Chứng minh rằng: 10 1...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

30 tháng 7 2017

Chứng minh rằng: 10 1 + 10 100 - 1 - 10 100 là một số nguyên

#Toán lớp 11

1

CM

Cao Minh Tâm

30 tháng 7 2017

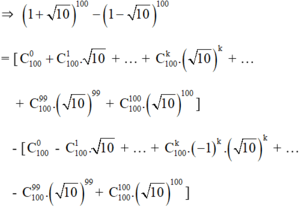
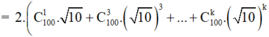
Giải bài 6 trang 58 sgk Đại số 11 | Để học tốt Toán 11

Giải bài 6 trang 58 sgk Đại số 11 | Để học tốt Toán 11

Giải bài 6 trang 58 sgk Đại số 11 | Để học tốt Toán 11

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

3 tháng 4 2017

Chứng minh rằng :

a) \(11^{10}-1\) chia hết cho 100

b) \(101^{100}-1\) chia hết cho 10 000

c) \(\sqrt{10}\left[\left(1+\sqrt{10}\right)^{100}-\left(1-\sqrt{10}\right)^{100}\right]\) là một số nguyên

#Toán lớp 11

3

LT

Lê Thiên Anh

3 tháng 4 2017

a) 1110 – 1 = (1 + 10)10 – 1 = (1 + C110 10 + C210102 + … +C910 109 + 1010) – 1

= 102 + C210102 +…+ C910 109 + 1010.

Tổng sau cùng chia hết cho 100 suy ra 1110 – 1 chia hết cho 100.

b) Ta có

101100 – 1 = (1 + 100)100 - 1

= (1 + C1100 100 + C2100 1002 + …+C99100 10099 + 100100) – 1.

= 1002 + C21001002 + …+ 10099 + 100100.

Tổng sau cùng chia hết cho 10 000 suy ra 101100 – 1 chia hết cho 10 000.

c) (1 + √10)100 = 1 + C1100 √10 + C2100 (√10)2 +…+ (√10)99 + (√10)100

(1 - √10)100 = 1 - C1100 √10 + C2100 (√10)2 -…- (√10)99 + (√10)100

√10[(1 + √10)100 – (1 - √10)100] = 2√10[C1100 √10 + C3100 (√10)3 +…+ . (√10)99]

= 2(C1100 10 + C3100 102 +…+ 1050)

Tổng sau cùng là một số nguyên, suy ra √10[(1 + √10)100 – (1 - √10)100] là một số nguyên.

BT

Bùi Thị Vân

23 tháng 5 2017

a) \(11^{10}-1=\left(10+1\right)^{10}-1\)\(=C^0_{10}10^{10}+C^1_{10}10^9+...+C^9_{10}10+C^{10}_{10}-1\)
\(=10^{10}+C^1_{10}10^9+...+C^8_{10}10^2+10.10\) chia hết cho 100.
b) \(\left(101\right)^{100}-1=\left(100+1\right)^{100}-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^1_{100}100+C_{100}^{100}100^0-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+100.100+1-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+10000\) chia hết cho 10000.

LL

Linh Lê

29 tháng 9 2019

Chứng minh :

\(\frac{1}{10}.C^9_{100}=\frac{1}{100}.C^{10}_{101}\)

#Toán lớp 11

0

HT

Hoàng Trung Thành

15 tháng 2 2020 - olm

cho sô thực a sao cho a+\(\frac{1}{a}\)là số nguyên .chứng minh rằng \(a^n+\frac{1}{a^n}\)là số nguyên

#Toán lớp 11

0

BT

Bình Trần Thị

31 tháng 8 2016

chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình y = \(\frac{x}{3}\) với đồ thị của hàm số y = \(\sin x\) đều cách gốc tọa độ 1 khoảng nhỏ hơn \(\sqrt{10}\) .

#Toán lớp 11

0

BT

Bình Trần Thị

2 tháng 9 2016

chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình y = \(\frac{x}{3}\) với đồ thị của hàm số y = \(\sin x\) đều cách gốc tọa độ 1 khoảng nhỏ hơn \(\sqrt{10}\) .

#Toán lớp 11

0

BT

Bình Trần Thị

4 tháng 9 2016

chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình y = \(\frac{x}{3}\) với đồ thị của hàm số y = \(\sin x\) đều cách gốc tọa độ 1 khoảng nhỏ hơn \(\sqrt{10}\) .

#Toán lớp 11

0

BT

Bình Trần Thị

5 tháng 9 2016

chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình y = \(\frac{x}{3}\) với đồ thị của hàm số y = \(\sin x\) đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt{10}\) .

#Toán lớp 11

1

C

Curtis

5 tháng 9 2016

Bạn tự vẽ hình nhé !

* Cách 1 : Đường thẳng \(y=\frac{x}{3}\) đi qua các điểm E( - 3 ; - 1 ) và F ( 3 ; 1 )

Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải { ( x ; y ) | - 1 \(\leq\) y \(\leq\) 1 } ( dải này chứa đô thị của hàm số y = sinx ).

Vậy các giao điểm của đường thẳng \(y=\frac{x}{3}\) với đô thị của hàm số y = sinx phải thuộc đoạn thẳng EF ; mọi điểm của đoạn thẳng này cách O một khoảng không dài hơn \(\sqrt{9+1}=\sqrt{10}\)

( và rõ ràng E , F không thuộc đô thị của hàm số y = sinx ).

* Cách 2 : Gọi A( x₀ ; y_o ) là giao điểm của đồ thị hàm số y = sinx vậy y = \(\frac{x}{3}\)

Ta có : \(y_0=sinx_0=>\left|y_0\right|\le1\)

\(sinx_0=\frac{x_0}{3}=>x_0=3sinx_0=>\left|x_0\right|\le3\)

Khoảng cách từ A( x₀ ; y₀ ) đến gốc tọa độ O là

\(OA=\sqrt{x^2_0}+y^2_0\le\sqrt{\left(3sinx_0\right)^2+y^2_0}\)

\(\le\sqrt{\left(3\right)^2+1^2}=\sqrt{10}\)

SG

Sách Giáo Khoa

10 tháng 4 2017

Chứng minh rằng nếu n là số nguyên tố thì với \(r=1,2,n,.....n-1\), ta có \(C_n^r\) chia hết cho \(n\)

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

19 tháng 5 2017

Có thể chứng minh đẳng thức sau :

\(rC^r_n=nC^{r-1}_{n-1}\) \(\left(r=1,2,3,....,n-1\right)\)

Vì \(n\) là số nguyên tố và \(r< n\), nên \(n\) là ước của \(C^r_n\)

SG

Sách Giáo Khoa

4 tháng 4 2017

Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau 1 khoảng thời gian \(T=24000\) năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã) Gọi \(u_n\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n a) Tìm số hạng tổng quát \(u_n\) của dãy số \(\left(u_n\right)\) b) Chứng minh...

#Toán lớp 11

1

DP

Đặng Phương Nam

4 tháng 4 2017

a) Nhận xét: u₁= $\frac{1}{2}$ ; u₂= $\frac{1}{4}$ ; u₃= $\frac{1}{8}$ ; ... u_n= $\frac{1}{2^{n}}$ .

Điều này chứng minh đơn giản bằng quy nạp.

b) lim u_n= lim ( $\frac{1}{2}$ )ⁿ= 0 = vì lim qⁿ = 0 nếu |q| < 1.

c) Đổi 10^-6g = $\frac{1}{10^{6}}$ . $\frac{1}{10^{3}}$ kg = $\frac{1}{10^{9}}$ kg.

Muốn có u_n= $\frac{1}{2^{n}}$ < $\frac{1}{10^{9}}$ , ta cần chọn n₀sao cho 2ⁿ₀> 10⁹. Chẳng hạn, với n₀= 36, thì

2³⁶= (2⁴)⁹ = 16 ⁹> 10⁹. Nói cách khác, sau chu kì thứ 36 (nghĩa là sau 36.24000 = 864 000 (năm), chúng ta không còn lo lắng về sự độc hại của khối lượng chất phóng xạ còn lại.

SG

Sách Giáo Khoa

11 tháng 4 2017

Cho dãy số \(\left(u_n\right)\) với \(u_n=3-2n\)

a) Xét tính tăng, giảm của dãy số

b) Chứng minh rằng dãy số trên là cấp số cộng

c) Tính tổng của 100 số hạng đầu của dãy số

#Toán lớp 11

0