Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

+ PT dao động của 2 vật: x 1 = 5 cos ω t x 2 = 5 3 cos ω t + π 2
+ Khi đồ thị cắt nhau, tức là 2 vật cùng nằm trên một đường thẳng vuông góc với Ox, khi đó: x 2 − x 1 = 0
⇒ ω t = − π 6 + k π ⇒ t 1 = 5 π 6 ω k = 1 t 2 = 23 π 6 ω k = 4 ⇒ ω = 3 π 1 , 08
+ Gọi d là khoảng cách giữa hai vật: d 2 = x 2 − x 1 2 + 5 2 ⇒ x 2 − x 1 = 5 2
+ Bấm máy x 2 − x 1 = 10 cos ω t + 2 π 3
+ Nhận thấy lần thứ 2016 = lần thứ 4 + 2012 4
+ Thời gian cần tính: t = 19 T 24 + 503 T = 362 , 73 s
Chọn đáp án A

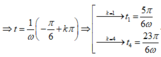
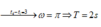
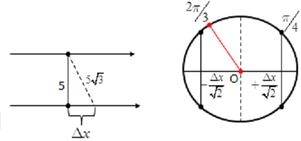
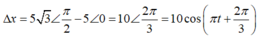
*Ở thời điểm t bất kì nếu hai chất điểm cách nhau 5 3 thì khoảng cách theo phương Ox sẽ là:
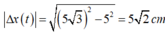
*Một chu kì có 4 lần thõa mãn ∆ x = 5 2 nên lần thứ 2018 sẽ là:
(Số lần / 4 ) = 504 + 2 (1 chu kì có 4 lần ∆ x thỏa mãn ).
*Dựa vào VTLG ta có thời gian lần thứ 2018 thỏa ∆ x = 5 2 cm
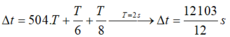

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M O1 O2 d1 d2
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)
 chọn A
chọn A
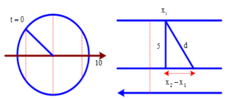
Đáp án B
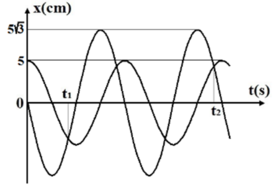
Từ đồ thị ta viết được phương trình của x1 và x2 là
Từ đồ thì ta thấy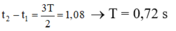
Gọi d là khoảng cách giữa 2 vật: d2 = 52 + (x2 - x1)2
Sử dụng máy tính tổng hợp phương trình trên ta được
Trong 1T tính từ t = 0 thì giá trị trên đạt được 4 lần
→ Lần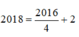
+ Vật đạt 2 lần nữa khi ở vị trí điểm A
Góc quét từ t = 0 đến A là j = 600 + 450 = 1050
+ Tổng thời gian là: