
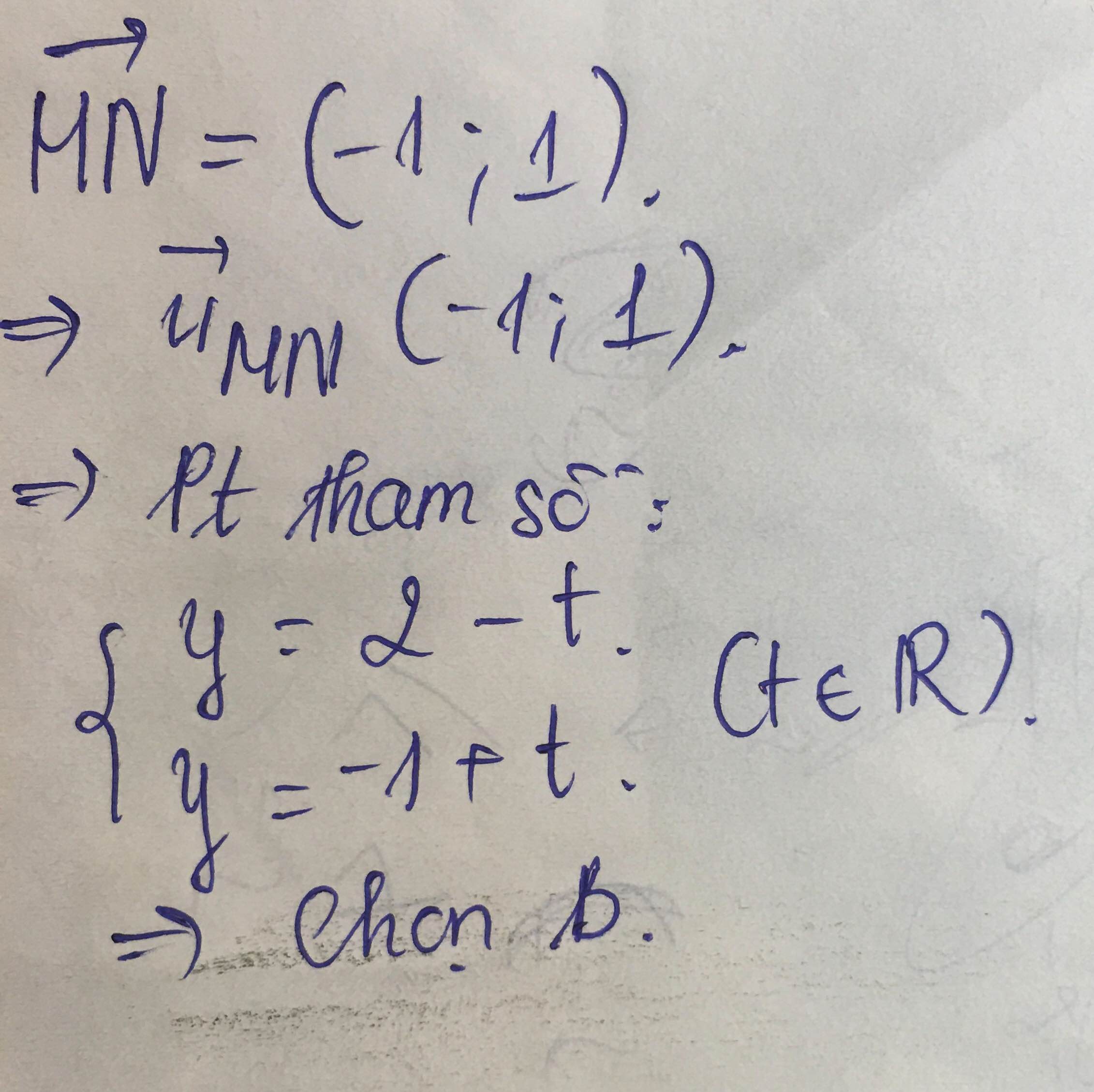
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

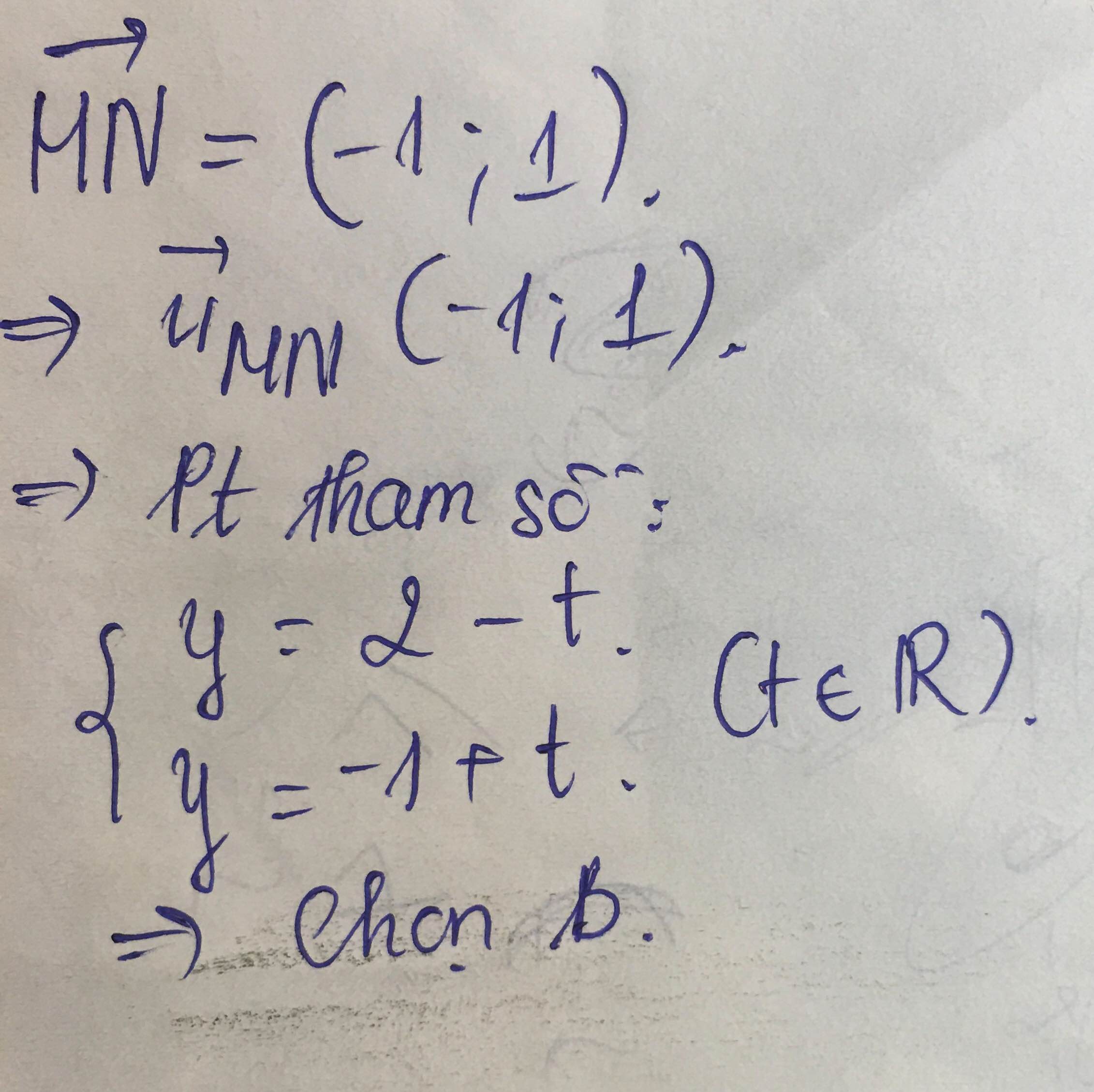

1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2

Lời giải:
Viết lại đt $(d_1)$:
$x+2y=m+1-6t+6t$
$\Leftrightarrow x+2y=m+1$
Ta thấy $M(-2,2)\in (d_2)$. Nếu $(d_2)\equiv (d_1)$ thì:
$M(-2,2)\in (d_1)$
$\Leftrightarrow -2+2.2=m+1$
$\Leftrightarrow m=1$
Thay giá trị $m$ vừa tìm được vào 2 ptđt ban đầu thì:
$(d_1)$: $x+2y=2$
$(d_2)$: \(\left\{\begin{matrix} x=-2-2t\\ y=2+t\end{matrix}\right.\)
$\Rightarrow x+2y=-2-2t+2(2+t)=2$ (trùng với $(d_1)$)
Vậy $m=1$

Lời giải:
Đường thẳng $(d_1)$ có VTCP là \(\overrightarrow{u_1}=(-\sqrt{2}; \sqrt{2})\)
Đường thẳng $(d_2)$ có VTCP là \(\overrightarrow{u_2}=(-2;2)\)
\(\Rightarrow \overrightarrow{u_2}=\sqrt{2}.\overrightarrow{u_1}(1)\)
Gọi $A(2,2)$ thuộc $(d_1)$
Thay tọa độ điểm $A$ vào $(d_2)$ ta thấy không thỏa mãn nên $A\not\in (d_2)(2)$
Từ $(1);(2)\Rightarrow (d_1); (d_2)$ song song với nhau.

1: \(x\in\left(1;5\right)\cup\left(-\infty;-2\right)\)
2: x>1
4: \(x\in\left(-2;+\infty\right)\)

Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Tại sao từ cos 450=\(\dfrac{\sqrt{2}}{2}\) thì lại => a=3b hoặc a=\(\dfrac{-b}{3}\) ạ ?