


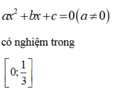
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



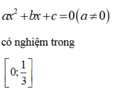

Lời giải:
$f(x)=ax^2+bx+c$ liên tục trên $[0; \frac{1}{3}]$
$f(0)=c$
$f(\frac{1}{3})=\frac{1}{9}a+\frac{1}{3}b+c$
$\Rightarrow 18f(\frac{1}{3})=2a+6b+18c$
$\Rightarrow f(0)+18f(\frac{1}{3})=2a+6b+19c=0$
$\Rightarrow f(0)=-18f(\frac{1}{3})$
$\Rightarrow f(0).f(\frac{1}{3})=-18f(\frac{1}{3})^2\leq 0$
$\Rightarrow$ pt luôn có nghiệm trong $[0; \frac{1}{3}]$ (đpcm)

Đặt \(f\left(x\right)=x^3+ax^2-bx+c\)
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+ax^2-bx+c\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{a}{x}-\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=+\infty\)
\(\Rightarrow\) Luôn tồn tại \(x=m>0\) đủ lớn sao cho \(f\left(m\right)>0\)
\(\lim\limits_{x\rightarrow-\infty}\left(x^3+ax^2-bx+c\right)=\lim\limits_{x\rightarrow-\infty}x^3\left(1-\dfrac{a}{x}+\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=-\infty\)
\(\Rightarrow\) Luôn tồn tại \(x=n< 0\) đủ nhỏ sao cho \(f\left(n\right)< 0\)
\(\Rightarrow f\left(m\right).f\left(n\right)< 0\Rightarrow f\left(x\right)=0\) luôn có nghiệm

- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
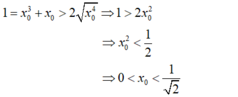

Đặt \(f\left(x\right)=ax^{3\:}+bx^2+cx+d\left(a\ne0\right)\)
Nếu \(a< 0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)\in\left(-\infty;+\infty\right)\), với \(x\in\left(-\infty;+\infty\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm
Nếu \(a>0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm
Chứng minh rằng các phương trình sau luôn có nghiệm: a)x^5 - 3x+3=0 b)x^5+x-1=0 c)x^4+x^3-3x^2+x+1=0

Lời giải:
a) $f(x)=x^5-3x+3$ liên tục trên $R$
$f(0)=3>0; f(-2)=-23<0\Rightarrow f(0)f(-2)<0$
Do đó pt $f(x)=0$ có ít nhất 1 nghiệm thuộc $(-2;0)$
Nghĩa là pt đã cho luôn có nghiệm.
b) $f(x)=x^5+x-1$ liên tục trên $R$
$f(0)=-1<0; f(1)=1>0\Rightarrow f(0)f(1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(0;1)$
Hay pt đã cho luôn có nghiệm.
c) $f(x)=x^4+x^3-3x^2+x+1$ liên tục trên $R$
$f(0)=1>0; f(-1)=-3<0\Rightarrow f(0)f(-1)<0$
$\Rightarrow f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(-1;0)$
Hay pt đã cho luôn có nghiệm.

Cần điều kiện \(a;b;c\) có ít nhất 2 số khác 0
- Với \(a=0\Rightarrow x=-\frac{c}{b}\) mà \(6b+19c=0\Rightarrow-\frac{c}{b}=\frac{6}{19}\Rightarrow x=\frac{6}{19}>0\)
- Với \(c=0\Rightarrow2a+6b=0\Rightarrow-\frac{b}{a}=\frac{1}{3}\)
\(ax^2+bx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\frac{b}{a}=\frac{1}{3}>0\end{matrix}\right.\)
- Với \(abc\ne0\)
\(2a+6b+19c=0\Rightarrow2\left(a+3b\right)=-19c\Rightarrow a+3b=-\frac{19}{2}c\)
Đặt \(f\left(x\right)=ax^2+bx+c\)
Ta có: \(f\left(0\right)=c\) ; \(f\left(\frac{1}{3}\right)=\frac{a}{9}+\frac{b}{3}+c\)
\(\Rightarrow f\left(0\right).f\left(\frac{1}{3}\right)=c\left(\frac{a}{9}+\frac{b}{3}+c\right)=\frac{1}{9}c\left(a+3b+9c\right)\)
\(=\frac{1}{9}c\left(-\frac{19}{2}c+9c\right)=-\frac{1}{18}c^2< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\frac{1}{3}\right)\)
Vậy phương trình luôn có một nghiệm dương

thôi để giải luôn
Xét phương trình: \(x^3+ax^2+bx+c=0\left(1\right)\)
Đặt : \(f\left(x\right)=x^3+2x^2+bc+c\)
Từ giả thiết \(\left\{{}\begin{matrix}4a+c>8+2b\Rightarrow-8+4a-2b+c>0\Rightarrow f\left(-2\right)>0\\a+b+c< -1\Rightarrow1+a+b+c< 0\Rightarrow f\left(1\right)< 0\end{matrix}\right.\)
Do đó \(f\left(-2\right).f\left(1\right)< 0\) nên pt (1) có ít nhất một nghiệm trong \(\left(-2;1\right)\)
Ta nhận thấy:
\(\overset{lim}{x\rightarrow-\infty}f\left(x\right)=-\infty\) mà \(f\left(-2\right)>0\) nên phương trình (1) có ít nhất một nghiệm \(\alpha\in\left(-\infty;-2\right)\)
Tương tự: \(\overset{lim}{x\rightarrow+\infty}f\left(x\right)=+\infty\) mà \(f\left(1\right)< 0\) nên phương trình (1) có ít nhất một nghiệm \(\beta\in\left(1+\infty\right)\)
Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm nên pt trên sẽ có 3 nghiệm thực phân biệt.