Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

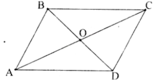
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
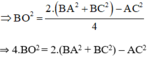
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
A B C D a b n m

Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm

ta có \(\hept{\begin{cases}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\Rightarrow AC^2=AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{BC}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}\Rightarrow BD^2=BA^2+AD^2+2\overrightarrow{BA}.\overrightarrow{AD}\end{cases}}\)
mà \(\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{BA}.\overrightarrow{AD}=\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{AB}.\overrightarrow{AD}=0\)
Do đó \(AC^2+BD^2=2AB^2+2BC^2\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!