Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).
A B C D P M
a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).
Tham khảo:
Dễ thấy: \(\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} \); \(\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} \)
Tương tự: \(\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} \); \(\overrightarrow {OD} = \overrightarrow {ON} + \overrightarrow {ND} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ND} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ON} + \overrightarrow {NC} + \overrightarrow {ND} } \right)\\ = \overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {ON} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 \\ = \overrightarrow 0 .\end{array}\)
A B C D I J
Áp dụng tính chất trung điểm ta có:
Do J là trung điểm của BD nên \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}\).
Theo quy tắc ba điểm: \(\overrightarrow{IB}=\overrightarrow{IA}+\overrightarrow{AB}\)
\(\overrightarrow{ID}=\overrightarrow{IC}+\overrightarrow{CD}\).
Vì vậy: \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{IC}+\overrightarrow{CD}\)
\(=\left(\overrightarrow{IA}+\overrightarrow{IC}\right)+\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\)
\(=\overrightarrow{AB}+\overrightarrow{CD}\) (ĐPCM).
\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
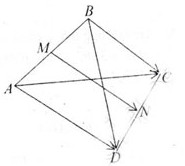
N là trung điểm của CD:
2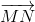
=
+ 
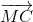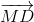(1)
Theo quy tắc 3 điểm, ta có:
= 
+
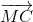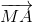(2)
= 
+ 
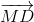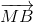(3)
Từ (1), (2), (3) ta có: 2= +++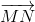
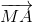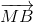
vì M là trung điểm của Ab nên: + =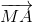 
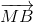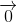
Suy ra : 2 = +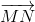
Chứng minh tương tự, ta có 2 =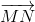 
+
Chú ý: Sau khi chứng minh 2 C = + ta chỉ cần chứng minh thêm + = + cũng được
Ta có: + = 
++
+
= +++= ++
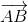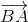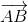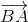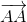
Vì 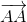= 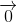nên ta có: +=+
và 2= + = +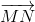
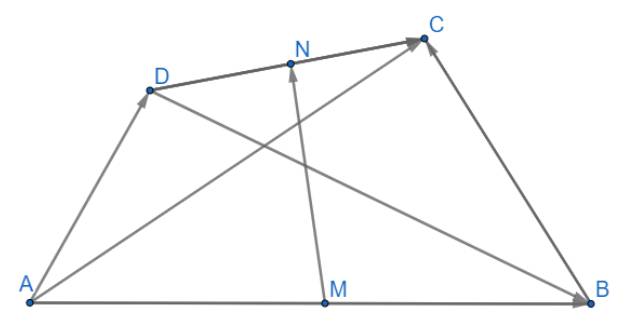
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)
A B C D M N Q P
a)
MN là đường trung bình của tam giác ABC nên \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\).
QP là đường trung bình của tam giác ABC nên \(\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\).
Vậy \(\overrightarrow{MN}=\overrightarrow{QP}\).
b) Giả sử:
\(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}\Leftrightarrow\overrightarrow{MP}-\overrightarrow{MN}-\overrightarrow{MQ}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MP}+\overrightarrow{NM}+\overrightarrow{QM}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{QM}+\overrightarrow{MP}\right)+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{MN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{QP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\) ( Điều giả sử đúng).
Vậy \(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}.\)