Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2022/2023 . (9/13 - 7/11) + 2022/2023 . (17/13- 4/17)
= 2022/2023 . 190/43 + 2022/2023 . 237/221
= 2022/2023 . (190/43 + 237/221)
= 2022/2023 . 52181/9503
= 105509982/19224569
Sửa: \(\dfrac{2022}{2023}\cdot\left(\dfrac{9}{13}-\dfrac{7}{11}\right)+\dfrac{2022}{2023}\cdot\left(\dfrac{17}{13}-\dfrac{4}{11}\right)\)
\(=\dfrac{2022}{2023}\cdot\left(\dfrac{9}{13}-\dfrac{7}{11}+\dfrac{17}{13}-\dfrac{4}{11}\right)\)
\(=\dfrac{2022}{2023}\cdot\left(2-1\right)\)
\(=\dfrac{2022}{2023}\cdot1\)
\(=\dfrac{2022}{2023}\)

\(\dfrac{1}{R\left(x\right)}=\dfrac{1}{x\left(x+2\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}-\dfrac{1}{x+2}\right)\)
\(\Rightarrow S=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2022}-\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{2024}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
Một kết quả rất xấu

\(\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{9}-\dfrac{2023}{2024}\right)\)
\(=\dfrac{1}{9}-\dfrac{1}{9}+\dfrac{2023}{2024}\)
\(=\dfrac{2023}{2024}\)

\(\dfrac{x-2023}{6}+\dfrac{x-2023}{10}+\dfrac{x-2023}{15}+\dfrac{x-2023}{21}=\dfrac{8}{21}\)
\(\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\left(x-2023\right).\dfrac{8}{21}=\dfrac{8}{21}\)
\(x-2023=1\)
\(x=2024\)
Vậy..............
\(...\Rightarrow\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right)\left(\dfrac{35+21+14+1}{210}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}.\dfrac{210}{71}=\dfrac{80}{71}\)
\(\Rightarrow x-2023=\dfrac{80}{71}\Rightarrow x=\dfrac{80}{71}+2023=\dfrac{143713}{71}\)

a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)
\(\left(b-1\right)^{2024}>=0\forall b\)
Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)
Thay a=-1 và b=1 vào P, ta được:
\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)

`12 + 8 . (-1/2)^3 + [(2023)^0 : 1/2 ]^2`
`= 12 + 8 . (-1/8) + ( 1 : 1/2)^2`
`= 12 + (-8/8) + 2^2`
`= 12 + (-1) + 4`
`= 11 +4`
`=15`

a/
\(VT=\dfrac{\left(x+4\right)-\left(x+2\right)}{\left(x+2\right)\left(x+4\right)}+\dfrac{\left(x+8\right)-\left(x+4\right)}{\left(x+4\right)\left(x+8\right)}+\dfrac{\left(x+14\right)-\left(x+8\right)}{\left(x+8\right)\left(x+14\right)}=\)
\(=\dfrac{1}{x+2}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+8}+\dfrac{1}{x+8}-\dfrac{1}{x+14}=\)
\(=\dfrac{1}{x+2}-\dfrac{1}{x+14}=\dfrac{12}{\left(x+2\right)\left(x+14\right)}\)
\(\Rightarrow\dfrac{12}{\left(x+2\right)\left(x+14\right)}=\dfrac{x}{\left(x+2\right)\left(x+14\right)}\left(x\ne-2;x\ne-14\right)\)
\(\Rightarrow x=12\)
\(\dfrac{x}{2023}+\dfrac{x+1}{2022}+...+\dfrac{x+2022}{1}+2023=0\)
\(\dfrac{1}{2023}x+\dfrac{1}{2022}x+\dfrac{1}{2022}\cdot1+...+\dfrac{1}{1}x+\dfrac{1}{1}\cdot2022+2023=0\)
\(x\left(\dfrac{1}{2023}+\dfrac{1}{2022}+...+\dfrac{1}{1}\right)+\left(\dfrac{1}{2022}+\dfrac{2}{2021}+...+\dfrac{2022}{1}+2023\right)=0\)
\(x\left(\dfrac{1}{2023}+\dfrac{1}{2022}+...+\dfrac{1}{1}\right)=\dfrac{1}{2022}+\dfrac{2}{2021}+...+\dfrac{2022}{1}+2023\)
\(x=\dfrac{\dfrac{1}{2022}+\dfrac{2}{2021}+...+\dfrac{2022}{1}+2023}{\dfrac{1}{2023}+\dfrac{1}{2022}+...+\dfrac{1}{1}}\)
\(x=\dfrac{\dfrac{1}{2022}+\dfrac{2022}{2022}+\dfrac{2}{2021}+\dfrac{2021}{2021}+...+\dfrac{2022}{1}+\dfrac{1}{1}}{\dfrac{1}{2023}+\dfrac{1}{2022}+...+\dfrac{1}{1}}\)
\(x=\dfrac{\dfrac{2023}{2022}+\dfrac{2023}{2021}+...+\dfrac{2023}{1}}{\dfrac{1}{2022}+\dfrac{1}{2021}+...+\dfrac{1}{1}}=2023\)
Vậy x = 2023

\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2021}{2022}\cdot\dfrac{2022}{2023}\)
=1/2023
\(B=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2021}{2022}.\dfrac{2022}{2023}\)
\(=\dfrac{1.2.3...2022}{2.3.4...2023}=\dfrac{1}{2023}\)

\(D=\dfrac{\left|x\right|+2023}{\left|x\right|+2022}=\dfrac{\left|x\right|+2022}{\left|x\right|+2022}+\dfrac{1}{\left|x\right|+2022}\\ =1+\dfrac{1}{\left|x\right|+2022}\)
Nhận thấy : \(\left|x\right|\ge0\forall x\inℝ\)
\(\Rightarrow\left|x\right|+2022\ge2022\)
\(\Rightarrow\dfrac{1}{\left|x\right|+2022}\le\dfrac{1}{2022}\)
\(\Rightarrow D=1+\dfrac{1}{\left|x\right|+2022}\le1+\dfrac{1}{2022}=\dfrac{2023}{2022}\)
Dấu = xảy ra khi : \(\left|x\right|=0\Rightarrow x=0\)
Vậy GTLN của D là : \(\dfrac{2023}{2022}\) tại x=0
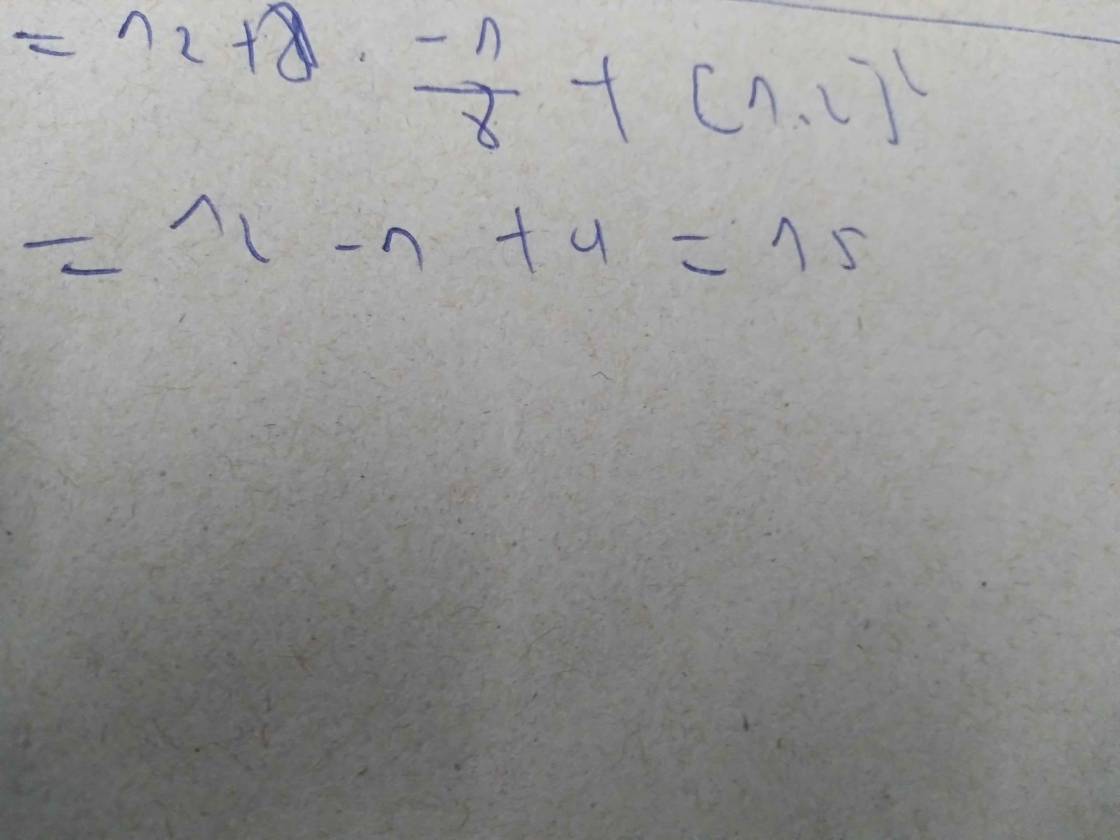
Sửa đề: \(B=\left(\dfrac{2008}{2023}-\dfrac{2023}{2008}\right)-\left(\dfrac{-15}{2003}-\dfrac{15}{2008}\right)\)
\(=\dfrac{2008}{2023}-\dfrac{2023}{2008}+\dfrac{15}{2003}+\dfrac{15}{2008}\)
=1-1
=0