Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

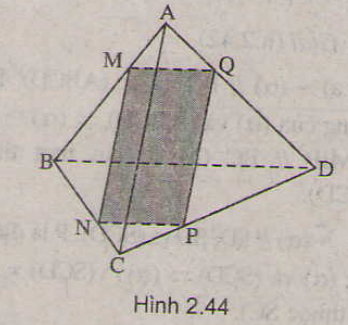
a/ Trong mp (BCD), nối BP cắt CD tại E
Trong mp (ABP), nối MP cắt AE kéo dài tại F (trong trường hợp MP không song song AE)
\(\Rightarrow F=MP\cap\left(ACD\right)\)
b/Nếu MN cắt BC, kéo dài MN cắt BC tại G
Nối GP cắt BD tại H
Trong mặt phẳng (ABD), nối MH cắt AD tại K (trong trường howph MH ko song song AD)
\(\Rightarrow K=AD\cap\left(MNP\right)\)
c/\(H=BD\cap\left(MNP\right)\)

a) S, I, J, G là điểm chunng của (SAE) và (SBD)
b) S, K, L là điểm chung của (SAB) và (SDE)

a/ Trong mặt phẳng (BCD), nối BO kéo dài cắt CD tại E
Trong mặt phẳng (ACD), nối AE cắt MN tại F
\(\Rightarrow F=MN\cap\left(ABO\right)\)
b/ Trong mặt phẳng (ABE), nối BF cắt AO tại P
\(\Rightarrow P=AO\cap\left(MNB\right)\)

a/ Gọi O là giao điểm AC và BD
Trong mặt phẳng (SBD), nối SO cắt BN tại I \(\Rightarrow I=BN\cap\left(SAC\right)\)
b/ Nối MD cắt AC tại P
Trong mặt phẳng (SMD), nối MN cắt SP tại J
\(\Rightarrow J=MN\cap\left(SAC\right)\)
c/ Ba mặt phẳng (SAC); (BCN), (SDM) cắt nhau theo 3 giao tuyến phân biệt CI, MN, SP.
Mà SP cắt MN tại J \(\Rightarrow\) CI đi qua J hay C;I;J thẳng hàng

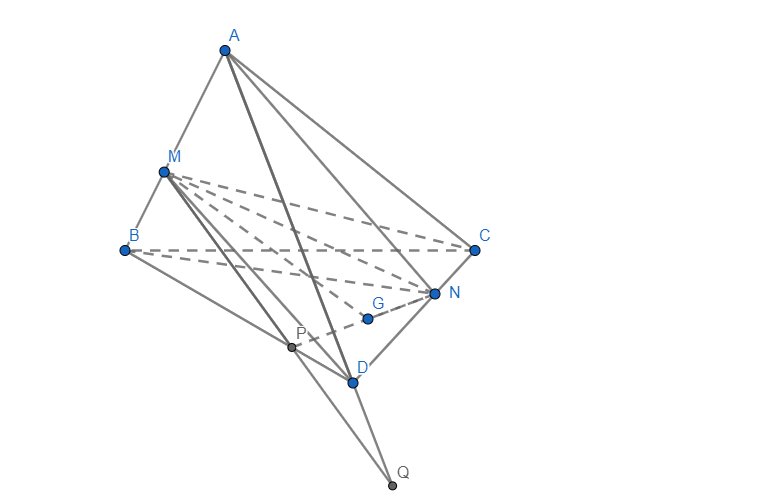
a) Ta có:
\(\left\{{}\begin{matrix}M\in\left(MCD\right)\\M\in AB\subset\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow M\in\left(MCD\right)\cap\left(NAB\right)\)
\(\left\{{}\begin{matrix}N\in CD\subset\left(MCD\right)\\N\in\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(MCD\right)\cap\left(NAB\right)\)
\(\Rightarrow MN=\left(MCD\right)\cap\left(NAB\right)\)
b) Trong mp(BCD), gọi \(P=NG\cap BD\)
Trong mp(BAD), gọi \(Q=PM\cap AD\)
Ta có:
\(\left\{{}\begin{matrix}N\in\left(GMN\right)\\N\in CD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(GMN\right)\cap\left(ACD\right)\)
Ta có:
\(\left\{{}\begin{matrix}Q\in MP\subset\left(GMN\right)\\Q\in AD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow Q\in\left(GMN\right)\cap\left(ACD\right)\)
\(\Rightarrow NQ=\left(GMN\right)\cap\left(ACD\right)\)