Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) \(\dfrac{12x^3}{y^4}.\dfrac{2y^5}{x^2}\)
\(=\dfrac{12.2.x^3.y^5}{x^2.y^4}\)
\(=\dfrac{24.x^2.x.y^4.y}{x^2.y^4}\)
\(=24xy\)
Vậy ...
b) \(\dfrac{5x-10}{4x-8}:\dfrac{2x+4}{4-2x}\)
\(=\dfrac{5\left(x-2\right)}{4\left(x-2\right)}:\dfrac{2\left(x+2\right)}{2\left(2-x\right)}\)
\(=\dfrac{5}{4}:\dfrac{x+2}{2-x}\)
\(=\dfrac{5}{4}.\dfrac{2-x}{x+2}\)
\(=\dfrac{5\left(2-x\right)}{4\left(x+2\right)}\)
\(=\dfrac{10-5x}{4x+8}\)
Vậy ...
c) \(\dfrac{3x+10}{x+3}.\dfrac{2x+4}{x+3}\)
\(=\dfrac{3x+10}{x+3}.\dfrac{2\left(x+2\right)}{x+3}\)
\(=\dfrac{\left(3x+10\right).2.\left(x+2\right)}{\left(x+3\right)^2}\)
Vậy ...

2)
a) \(\dfrac{1}{x}.\dfrac{6x}{y}\)
\(=\dfrac{6x}{xy}\)
\(=\dfrac{6}{y}\)
b) \(\dfrac{2x^2}{y}.3xy^2\)
\(=\dfrac{2x^2.3xy^2}{y}\)
\(=\dfrac{6x^3y^2}{y}\)
\(=6x^3y\)
c) \(\dfrac{15x}{7y^3}.\dfrac{2y^2}{x^2}\)
\(=\dfrac{15x.2y^2}{7y^3.x^2}\)
\(=\dfrac{30xy^2}{7x^2y^3}\)
\(=\dfrac{30}{7xy}\)
d) \(\dfrac{2x^2}{x-y}.\dfrac{y}{5x^3}\)
\(=\dfrac{2x^2.y}{\left(x-y\right).5x^3}\)
\(=\dfrac{2y}{5x\left(x-y\right)}\)

a) \(\dfrac{5x-1}{3x+2}=\dfrac{5x-7}{3x-1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{5x-1}{3x+2}=\dfrac{5x-7}{3x-1}\)
\(=\dfrac{5x-1-5x+7}{3x+2-3x+1}\)
\(=\dfrac{-1+7}{2+1}\)
\(=\dfrac{6}{3}\)
\(=2\)
Với \(\dfrac{5x-1}{3x+2}=2\)
\(\Rightarrow5x-1=2\left(3x+2\right)\)
\(\Rightarrow5x-1-2\left(3x+2\right)=0\)
\(\Rightarrow5x-1-6x-4=0\)
\(\Rightarrow-x-5=0\)
\(\Rightarrow x=-5\)

a: =>-4x>16
=>x<-4
c: =>20x-25<=21-3x
=>23x<=46
=>x<=2
d: =>20(2x-5)-30(3x-1)<12(3-x)-15(2x-1)
=>40x-100-90x+30<36-12x-30x+15
=>-50x-70<-42x+51
=>-8x<121
=>x>-121/8


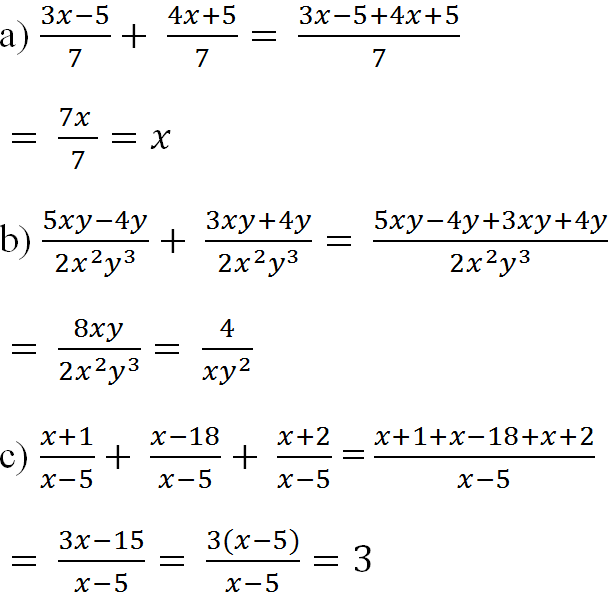

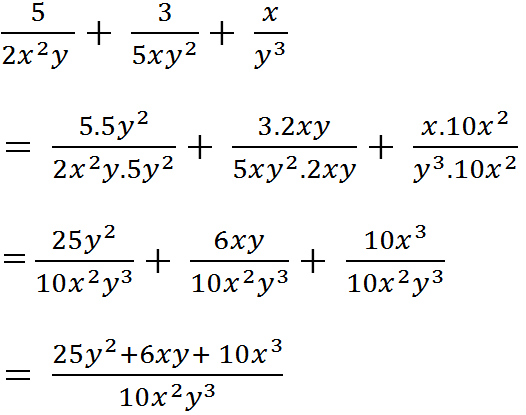

a, \(\dfrac{x+1}{3}+\dfrac{2x-1}{3}=\dfrac{x+1+2x-1}{3}=\dfrac{3x}{3}=x\)
b, \(\dfrac{5x-2y}{x^2-y^2}+\dfrac{y-4x}{x^2-y^2}=\dfrac{5x-2y+y-4x}{\left(x+y\right)\left(x-y\right)}=\dfrac{x-y}{\left(x+y\right)\left(x-y\right)}=\dfrac{1}{x+y}\)
c, \(\dfrac{x-1}{12x}+\dfrac{2x+7}{12x}+\dfrac{6-3x}{12x}=\dfrac{x-1+2x+7+6-3x}{12x}=\dfrac{12}{12x}=\dfrac{1}{x}\)
a,\(\dfrac{x+1_{ }+2x-1}{3}\)=\(\dfrac{2x}{3}\)
b,\(\dfrac{5x-2y+y-4x}{\left(x+y\right)\left(x-y\right)}\)=\(\dfrac{x-y}{\left(x+y\left(x-y\right)\right)}\)
c,\(\dfrac{x-1+2x+7+6-3x}{12x}\)=\(\dfrac{12}{12x}\)=\(\dfrac{1}{x}\)