Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đa thức biểu thị diện tích mảnh vườn là: \(xy\left(m^2\right)\)
b) Chiều rộng mảnh vườn mới là: \(x+2\left(m\right)\)
Chiều dài mảnh vườn mới là: \(y+3\left(m\right)\)
Đa thức biểu thị diện tích mảnh vườn mới là:
\(\left(x+2\right)\left(y+3\right)=xy+3x+3y+6\left(m^2\right)\)
c) Đa thưc biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu là:
\(xy+3x+3y+6-xy=3x+3y+6\left(m^2\right)\)
a, Diện tích mảnh vườn: x.y (m2)
b, Diện tích mảnh vườn mới: \(\left(x+2\right).\left(y+3\right)\left(m^2\right)\)
c, Diện tích phần lớn hơn:
\(\left(x+2\right)\left(y+3\right)-xy=\left(xy+2y+3x+6\right)-xy=2y+3y+6\left(m^2\right)\)

a) Đa thức biểu thị diện tích mảnh vườn:
a.(b - 6) (m²)
b) Diện tích mảnh vườn khi a = 14 m; b = 16 m:
14 . (16 - 6) = 14.10 = 140 (m²)

a) Biểu thức tính diện tích của mảnh vườn là: x.y (m2)
b) Chiều rộng mới là: (x + 2) (m)
Chiều dài mới là: (y - 3) (m)
Diện tích mảnh vườn mới là: (x + 2).(y – 3) (m2)
c) Đa thức biểu thị phần diện tích lớn hơn của mảnh vườn so với mảnh vườn ban đầu là:
(x + 2).(y – 3) – xy = xy – 3x + 2y – 6 – xy = 2y – 3x – 6 (m2)

a: s=(2x+5)(x-2)
\(=2x^2-4x+5x-10\)
\(=2x^2+x-10\)
b: Khi x=12 thì \(s=2\cdot12^2+12-10=2\cdot144+2=288+2=290\left(cm^2\right)\)

a) Độ dài cạnh mảnh vườn hình vuông sau khi mở rộng là: \(x + 10\) (m)
Diện tích mảnh vườn sau khi mở rộng là:
\(\left( {x + 10} \right)\left( {x + 10} \right) = {\left( {x + 10} \right)^2} = {x^2} + 2.x.10 + {10^2} = {x^2} + 20x + 100\) (\({m^2}\))
b) Độ dài cạnh mảnh vườn hình vuông trước khi mở rộng là: \(x - 5\) (m)
Diện tích mảnh vườn hình vuông trước khi mở rộng là: \(\left( {x - 5} \right)\left( {x - 5} \right) = {\left( {x - 5} \right)^2} = {x^2} - 2.x.5 + {5^2} = {x^2} - 10x + 25\) (\({m^2}\))

– Biểu thức tính diện tích mảnh vườn trên theo x và y là:
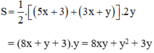
– Nếu x = 3 mét và y = 2 mét thì diện tích mảnh vườn là:
S = 8.3.2 + 22 + 3.2 = 58 (m2).

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a/ \(S=\left(5x+1\right)\left(5x-1\right)=25x^2-1\)
b/ \(S=25.2^2-1=99m^2\)
a) Đa thức biểu thị chu vi hình chữ nhật là:
\(\left(2x+y+2x-y\right)\cdot2=4x\cdot2=8x\left(m\right)\)
b) Đa thức biểu thị diện tích hình chữ nhật là:
\(\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\)
c) Diện tích của mảnh vườn là:
\(4\cdot3^2-2^2=32\left(m^2\right)\)
\(a,Chu.vi:2.\left(2x+y+2x-y\right)=2.4x=8x\left(m\right)\\ b,Diện.tích:\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\\ c,Thay:x=3;y=2.vào.biểu.thức.tính.diện.tích.thì.diện.tích.mảnh.vườn.là:\\ 4x^2-y^2=4.3^2-2^2=32\left(m^2\right)\)