Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

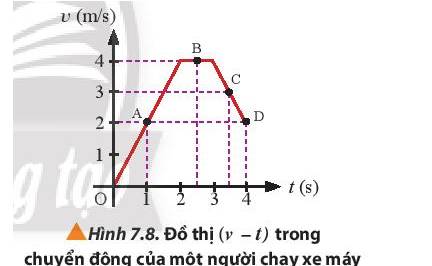
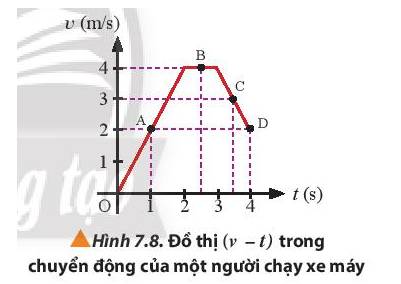
a) Gia tốc của người này tại các thời điểm là:
+ t = 1 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{2}{1} = 2(m/{s^2})\)
+ t = 2,5 s: \(a = 0 (m/{s^2})\)
+ t = 3,5 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{3-4}{{3,5-3}}=-2(m/{s^2})\)
b)
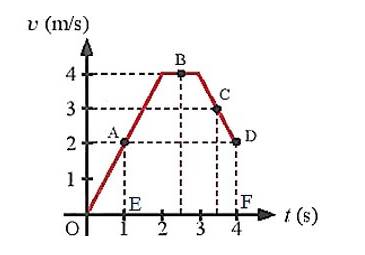
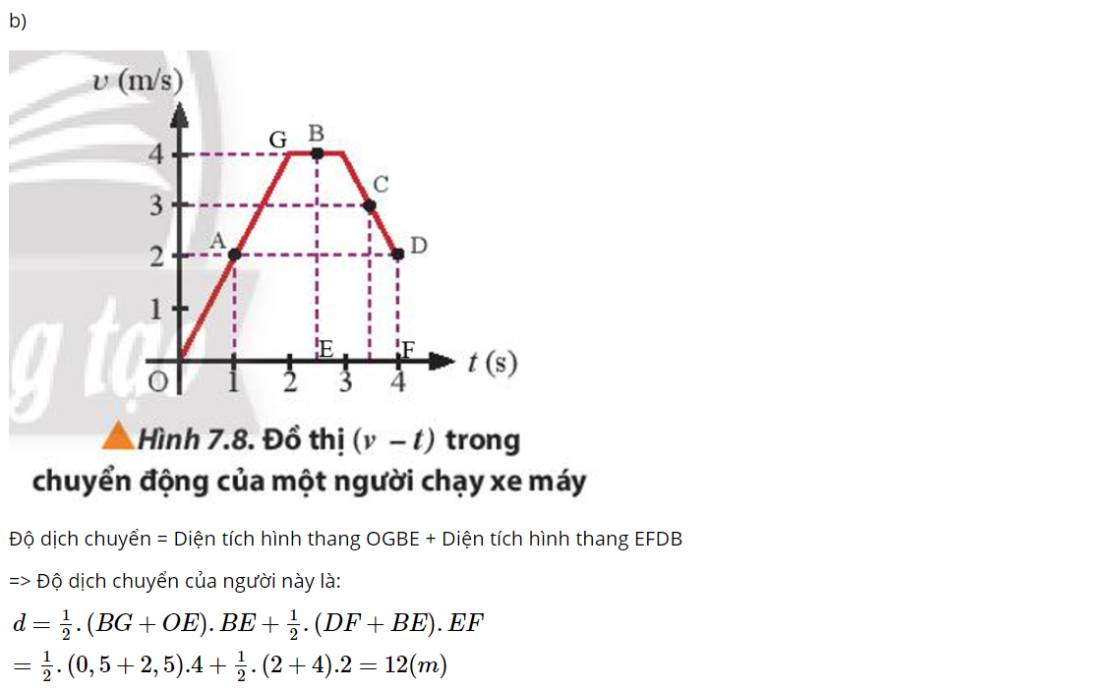
Độ dịch chuyển = Diện tích hình thang OGBE + Diện tích hình thang BKDH + Diện tích hình chữ nhật HDFE
=> Độ dịch chuyển của người này là:
\(\begin{array}{l}d = \frac{1}{2}.(BG + OE).BE + \frac{1}{2}.(BK + HD).BH\ + (EF.DF)\ = \frac{1}{2}.(0,5 + 2,5).4 + \frac{1}{2}.(0,5 + 1,5).2 + 2.1,5 = 11(m)\end{array}\)

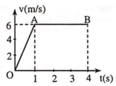
a) Gia tốc trên đoạn OA: a 1 = Δ v Δ t = 6 1 = 6 m/s2.
Trên đoạn AB chất điểm chuyển động thẳng đều nên gia tốc a 2 = 0 .
b) Quãng đường chất điểm đi trong 1s đầu tiên: s 1 = 1 2 a 1 t 1 2 = 1 2 .6.1 2 = 3 m.
Quãng đường chất điểm đi trong 2s kế tiếp: s 2 = v t 2 = 6.2 = 12 m.
Quãng đường chất điểm đi trong 3s đầu tiên: s 2 = v t 2 = 6.2 = 12 m.
c) Thời điểm mà chất điểm có vận tốc 2,4m/s: t = v a = 2 , 4 6 = 0 , 4 s.

1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
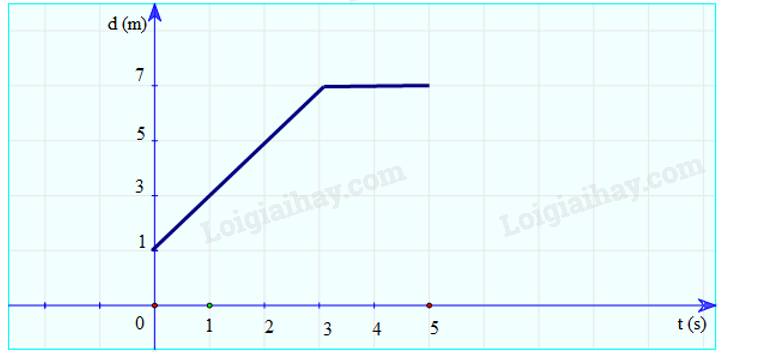
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
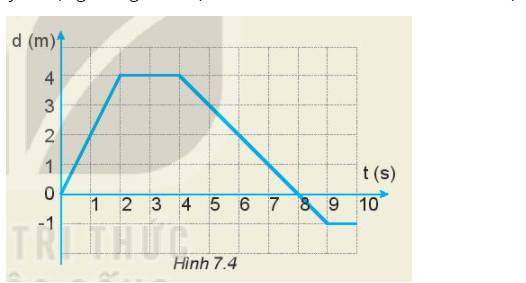
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.

a,ta có gốc A chiều + AB => X1=Xo+Vot+1/2at^2 vs Xo=0; Vo=10 ;a=-0.2(chậm dần)
=>X1=10t-0.1t^2
xe2 ở B có Xo=560 ,Vo=0 ,a=0.4 => X2=560-0.2t^2 ( xe 2 đi ngược lại B>A )
b,2 xe gặp nhau khi X1=X2 <=> 10t-0.1t^2=560-0.2t^2 <=> t=40(n) t=-140(l)
S1=Vot+1/2at^2=10*40 -0.1*40^2=240
S2=Vot+1/2at^2=0.2*40^2=320
c,tại thời điểm 2 xe gặp nhau t=40 => v xe1 lúc gặp nhau ;V1=Vo-at=10-0.2*40=2
V2=Vo +at=0.4*40=16
vẽ trục oy là v; ox là t trên oy lấy các điểm 2,10,16 trên ox lấy điểm 40 . vẽ đt x1 từ 10 đến giao điểm của 2 vs 40 . vẽ x2 từ 0 đến giao 16 vs 40

9. Trên một đường thẳng, tại hai điểm A và B cách nhau 10 km, có hai ô tô xuất phát cùng lúc và chuyển động cùng chiều. Ô tô xuất phát từ A có tốc độ 60 km/h và ô tô xuất phát từ B có tốc độ 40 km/h.
a) Lấy gốc tọa độ ở A, gốc thời gian là lúc xuất phát, hãy viết công thức tính quãng đường đi được và phương trình chuyển động của hai xe.
b) Vẽ đồ thị tọa độ - thời gian của hai xe trên cùng một hệ trục (x, t).
c) Dựa vào đồ thị tọa độ - thời gian để xác định vị trí và thời điểm mà xe A đuổi kịp xe B.
Trả lời:
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị
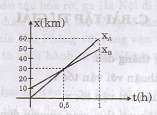
c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị

c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.


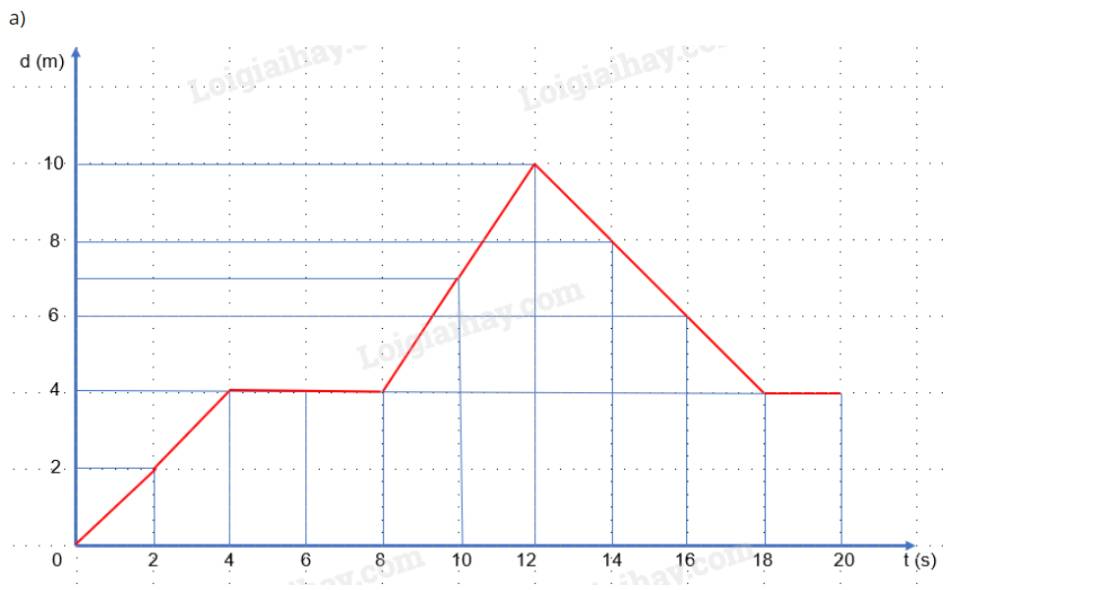



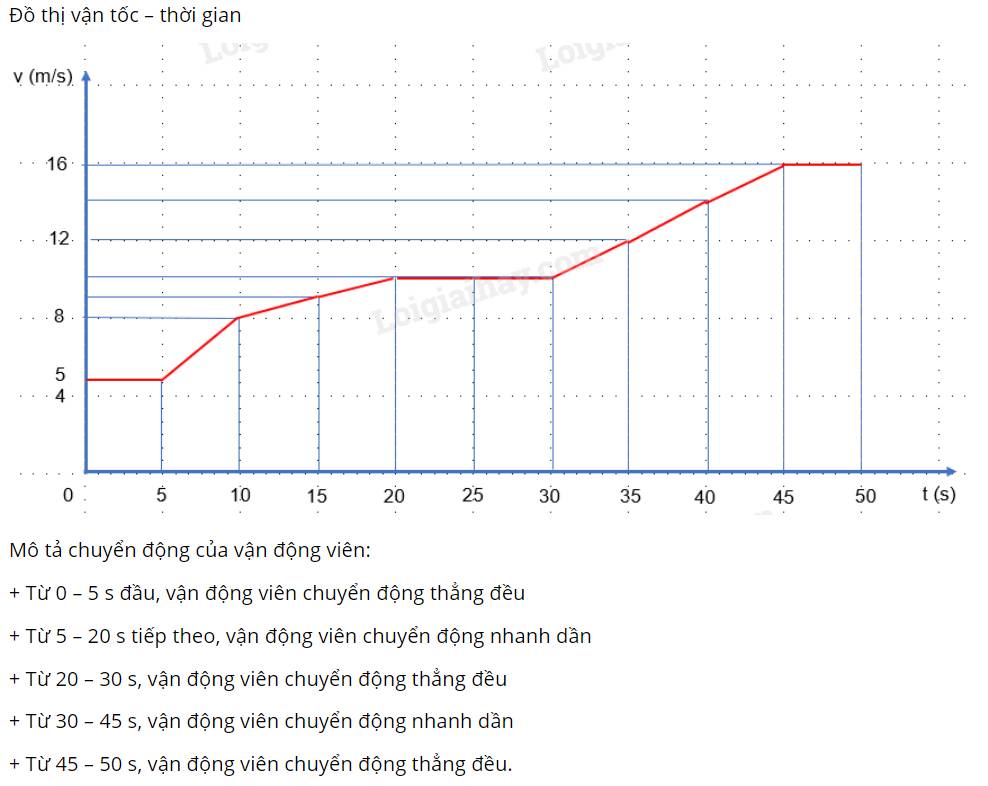
a) Vẽ đồ thị:
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)