Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

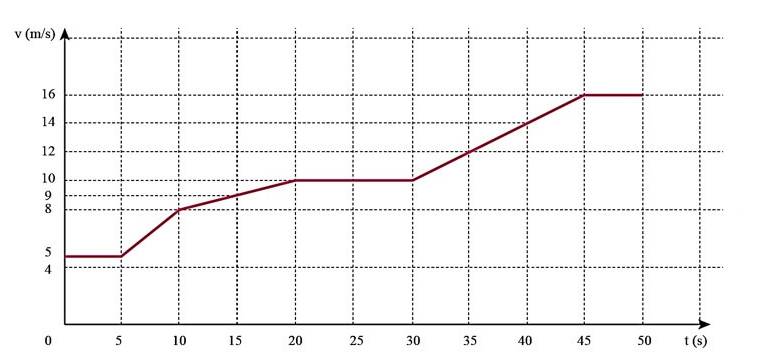
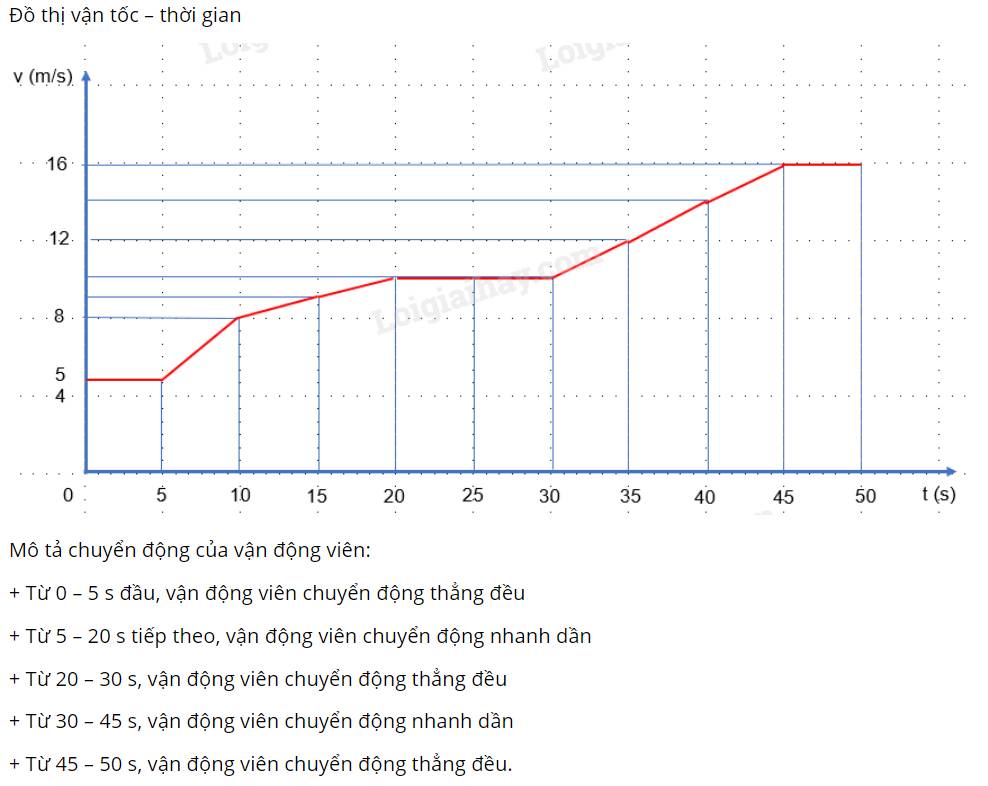
Mô tả chuyển động của vận động viên:
+ Từ 0 – 5 s đầu, vận động viên chuyển động thẳng đều
+ Từ 5 – 20 s tiếp theo, vận động viên chuyển động nhanh dần
+ Từ 20 – 30 s, vận động viên chuyển động thẳng đều
+ Từ 30 – 45 s, vận động viên chuyển động nhanh dần
+ Từ 45 – 50 s, vận động viên chuyển động thẳng đều.

1.
a) Mô tả chuyển động:
- Trong 2 giây đầu tiên: chuyển động thẳng đều với vận tốc 1 m/s.
- Từ giây thứ 2 đến giây thứ 4: chuyển động nhanh dần đều
- Từ giây 4 đến giây 7: chuyển động chậm dần
- Từ giây 4 đến giây 8: dừng lại
- Từ giây 8 đến giây 9: chuyển động nhanh dần theo chiều âm
- Từ giây 9 đến giây 10 chuyển động thẳng đều với vận tốc -1 m/s.
b) Quãng đường đi được và độ dịch chuyển:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\({s_2} = {d_2} = {s_1} + \frac{1}{2}(1 + 3).2 = 2 + 4 = 6\left( m \right)\)
- Sau 7 giây:
+ Quãng đường:
\({s_3} = {s_2} + \frac{1}{2}.3.\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
+ Độ dịch chuyển:
\({d_3} = {d_2} + \frac{1}{2}.(3).\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Quãng đường:
\({s_4} = {s_3} + s' = 10,5 + 0,5 + 1 = 12\left( m \right)\)
+ Độ dịch chuyển:
\({d_4} = {d_3} + d' = 10,5 - 0,5 - 1 = 9\left( m \right)\)
* Kiểm tra bằng công thức:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{3 - 1}}{{4 - 2}} = \frac{2}{2} = 1\left( {m/{s^2}} \right)\)
\({s_2} = {d_2} = {d_1} + {v_1}{t_1} + \frac{1}{2}at_1^2 = 2 + 1.2 + \frac{1}{2}{.1.2^2} = 6\left( m \right)\)
- Sau 7 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 3}}{{7 - 4}} = \frac{2}{2} = - 1\left( {m/{s^2}} \right)\)
+ Quãng đường và độ dịch chuyển từ giây 4 đến giây 7 là:
\(d' = s' = {v_0}t + \frac{1}{2}a{t^2} = 3.3 + \frac{1}{2}( - 1).{(7 - 4)^2} = 4,5\left( m \right)\)
=> Quãng đường và độ dịch chuyển đi được sau 7 giây là:
\({d_3} = {s_3} = {d_2} + d' = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Từ giây 7 – 8: đứng yên
+ Từ giây 8 – 9:
\(a = \frac{{ - 1 - 0}}{{9 - 8}} = - 1\left( {m/{s^2}} \right)\)
\(d = {v_0}t + \frac{1}{2}a{t^2} = 0.1 + \frac{1}{2}\left( { - 1} \right){.1^2} = - 0,5\left( m \right)\)
s = 0,5 m
+ Từ giây 9 – 10:
\(d = vt = - 1.1 = - 1\left( m \right)\)
s = 1 m
Suy ra: độ dịch chuyển và quãng đường đi được sau 10 giây lần lượt là:
\({d_4} = {d_3} - 0,5 - 1 = 10,5 - 0,5 - 1 = 9\left( m \right)\)
\({s_4} = {s_3} - 0,5 - 1 = 10,5 + 0,5 + 1 = 12\left( m \right)\)
=> Kiểm tra thấy các kết quả trùng nhau.
2.
a)
Gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích là:
\({v^2} - v_0^2 = 2{\rm{ad}} \Leftrightarrow a = \frac{{{v^2} - v_0^2}}{{2{\rm{d}}}} = \frac{{{0^2} - {{10}^2}}}{{2.20}} = - 2,5\left( {m/{s^2}} \right)\)
b)
Thời gian vận động viên đó cần để dừng lại kể từ khi cán đích là:
\(a = \frac{{\Delta v}}{{\Delta t}} \Leftrightarrow \Delta t = \frac{{\Delta v}}{a} = \frac{{0 - 10}}{{ - 2,5}} = 4\left( s \right)\)
c)
Vận tốc trung bình của người đó trên quãng đường dừng xe là:
\(v = \frac{d}{t} = \frac{{20}}{4} = 5\left( {m/s} \right)\)

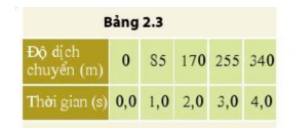
- Vẽ đồ thị độ dịch chuyển – thời gian: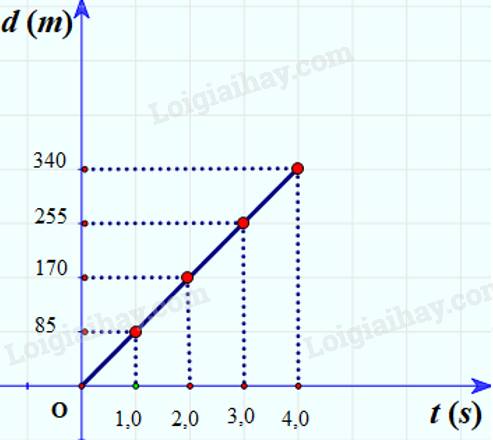
- Vận tốc của xe là:
\(v=\dfrac{d}{t}=85\left(m/s\right)\)

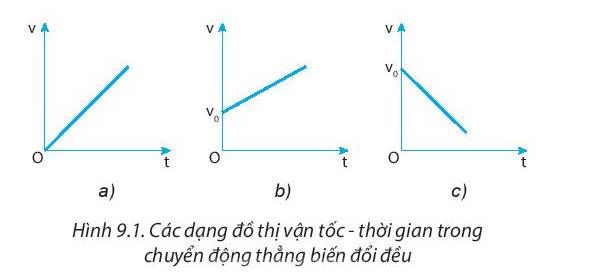
1. (a)
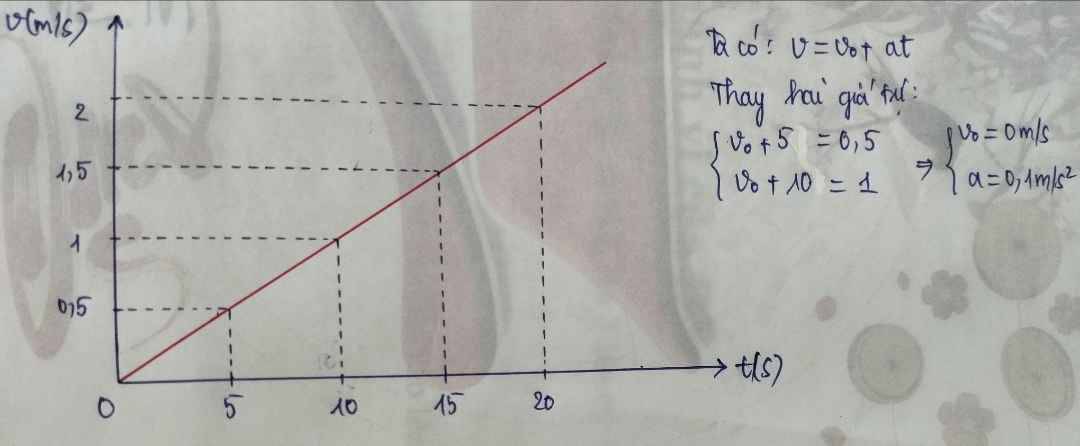
Đồ thị hình a là đường thẳng đi qua gốc tọa độ nên công thức mối liên hệ giữa v, a và t có dạng hàm số \(y=ax\). Công thức cần tìm là: \(v=at\left(a>0\right)\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a>0\right)\) (do đồ thị có dạng dấu sắc (đồng biến)) nên công thức cần tìm là: \(v=v_0+at\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a< 0\right)\) (do đồ thị có dạng dấu huyền (nghịch biến)) nên công thức cần tìm là: \(v=v_0-at\).
(b) Chuyển động nhanh dần đều là các chuyển động ở hình a, b. Chuyển động chậm dần đều là chuyển động ở hình c.
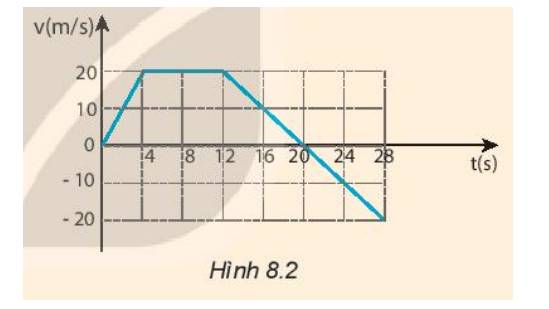
2. Từ thời điểm 0s đến 4s, tức 4s đầu, bạn đi đều với tốc độ 1,5m/s.
Từ thời điểm 4s đến 6s, tức 2s tiếp theo, bạn bắt đầu đi chậm lại từ tốc độ 1,5m/s xuống 0m/s.
Sau đó, từ thời điểm 6s đến 7s, tức 1s tiếp theo, bạn này dừng lại.
Trong 1s tiếp theo, từ thời điểm 7s đến 8s, bạn này bắt đầu đảo chiều đi (đi ngược lại so với chiều đi ban đầu) và bắt đầu chuyển động nhanh dần từ tốc độ 0m/s đến 0,5m/s.
Trong 1s sau đó, từ thời điểm 8s đến 9s, bạn này đi đều với tốc độ 0,5m/s với chiều đi như giây trước.
Cuối cùng, từ thời điểm 9s đến 10s, tức 1s cuối, bạn này đi chậm lại từ tốc độ 0,5m/s và dừng hẳn (tốc độ 0m/s).

1.
a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s
+ Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\)
+ Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\)
+ Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\)
+ Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\)
b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần.
2.
Gia tốc của con báo là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\)

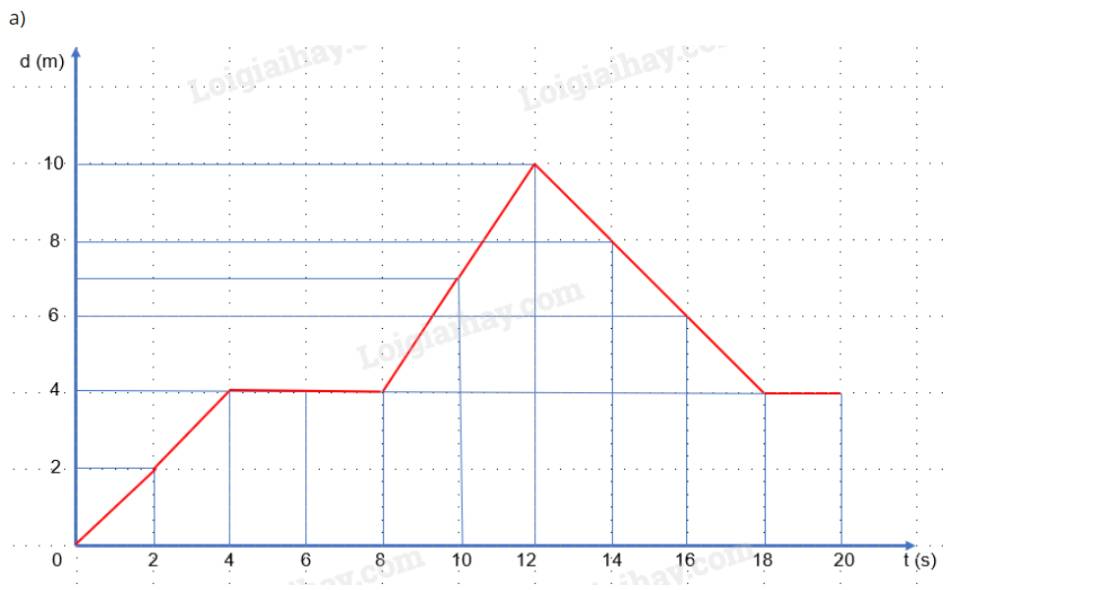
a) Vẽ đồ thị:
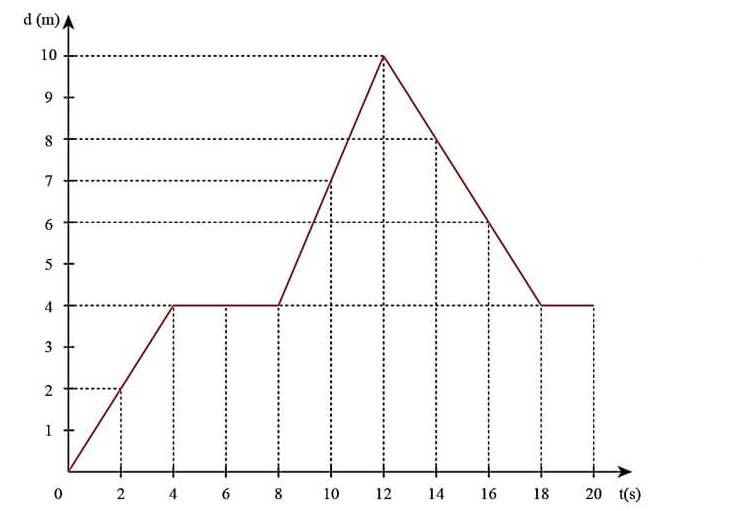
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)