
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)
k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)
m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)
\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)
\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)
Lời giải:
i.
\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)
k.
\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)
\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)
\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)
m.
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)
\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)

Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi



\(\Delta'=4-\left(m-1\right)=5-m\)
để pt có nghiệm kép khi \(5-m=0\Leftrightarrow m=5\)
chọn B
Phương trình có nghiệm kép khi:
\(\Delta'=4-\left(m-1\right)=0\Leftrightarrow5-m=0\)
\(\Rightarrow m=5\)

5:
a: \(\left\{{}\begin{matrix}x-2y=-m-7\\2x+y=3m-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=-2m-14\\2x+y=3m-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-5y=-5m-10\\x-2y=-m-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=m+2\\x=-m-7+2m+4=m-3\end{matrix}\right.\)
Thay x=m-3 và y=m+2 vào y=3x-1, ta được:
3(m-3)-1=m+2
=>3m-10=m+2
=>2m=12
=>m=6
b: A(x,y) nằm trong góc phần tư thứ II
\(\Leftrightarrow\left\{{}\begin{matrix}m-3< 0\\m+2>0\end{matrix}\right.\Leftrightarrow-2< m< 3\)
mà m nguyên
nên \(m\in\left\{-1;0;1;2\right\}\)

11) \(\dfrac{2\sqrt{3}-\sqrt{15}}{\sqrt{3}}\)
\(=\dfrac{\left(2\sqrt{3}-\sqrt{15}\right)\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}\)
\(=\dfrac{2\cdot\sqrt{3}\cdot\sqrt{3}-\sqrt{15}\cdot\sqrt{3}}{3}\)
\(=\dfrac{6-3\sqrt{5}}{3}\)
\(=2-\sqrt{5}\)
12) \(\dfrac{2\sqrt{2}+\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3}{5}\)
11: \(=\dfrac{\sqrt{3}\left(2-\sqrt{5}\right)}{\sqrt{3}}=2-\sqrt{5}\)
12: \(=\dfrac{3\sqrt{2}}{5\sqrt{2}}=\dfrac{3}{5}\)

\(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\Rightarrow C=\dfrac{x+3}{\sqrt{x}}=\sqrt{x}+\dfrac{3}{\sqrt{x}}\ge2\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}}}=2\sqrt{3}\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{3}{\sqrt{x}}\Rightarrow x=3\)

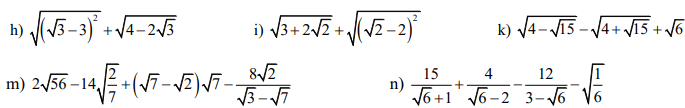






 giúp mình câu 11 , 12 v ạ mình camon
giúp mình câu 11 , 12 v ạ mình camon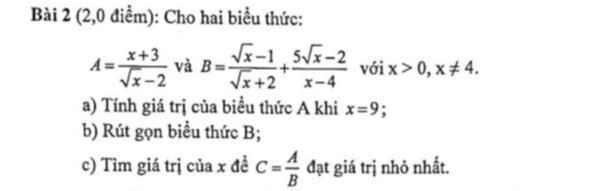 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Thay \(x=4-2\sqrt{3}\) vào P, ta được:
\(P=\dfrac{2\left(\sqrt{3}-1\right)+1}{\sqrt{3}-1+1}=\dfrac{2\sqrt{3}-2+1}{\sqrt{3}}=\dfrac{2\sqrt{3}-1}{\sqrt{3}}=\dfrac{6-\sqrt{3}}{3}\)
giúp mik câu 3 ạ