Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình nghĩ đề nó như thế này
\(\sqrt{a^2+b^2}-\sqrt{c^2+d^2}\ge\sqrt{\left(a+c\right)^2-\left(b+d^{ }\right)^2}\)
hai zế BĐT ko âm nên bình phương 2 zế ta có
\(a^2+b^2+c^2+d^2+2\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge a^2+2ac+c^2+b^2+2bd+d^2\)
\(\Leftrightarrow\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge ac+bd\left(1\right)\)
Nếu \(ac+bd< 0\)thì BĐT đc c/m
Nêu \(ac+bd\ge0\left(1\right)\Leftrightarrow\left(a^2+b^2\right)\left(c^2+d^2\right)\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2c^2+a^2d^2+b^2c^2+b^2d^2\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2d^2+b^2c^2-2acbd\ge0\Leftrightarrow\left(ad-bc\right)^2\ge0\)( luôn đúng )
dấu = xảy ra khi \(ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)

a: Hàm số nghịch biến trên R
b: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2-4x_1+5-x_2^2+4x_2-5}{x_1-x_2}\)
\(=x_1+x_2-4\)
Trường hợp 1: x<=2
\(\Leftrightarrow x_1+x_2-4< =0\)
Vậy: Hàm số nghịch biến khi x<=2

3.
Do M là trung điểm BC \(\Rightarrow\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
K là trung điểm AB \(\Rightarrow\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{BA}\)
Do đó:
\(\overrightarrow{AN}+\overrightarrow{CM}-\overrightarrow{KB}=\overrightarrow{AN}+\overrightarrow{CM}+\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BA}=\overrightarrow{0}\)
4.
\(\overrightarrow{BC}=\left(6;-2\right)\)
Gọi \(A'\left(x;y\right)\Rightarrow\overrightarrow{BA'}=\left(x+3;y-1\right)\)
Do A' thuộc BC \(\Rightarrow\overrightarrow{BA'}\) và \(\overrightarrow{BC}\) cùng phương
\(\Rightarrow\dfrac{x+3}{6}=\dfrac{y-1}{-2}\Rightarrow x=-3y\)
\(\Rightarrow A'\left(-3y;y\right)\Rightarrow\overrightarrow{AA'}=\left(-3y-2;y-4\right)\)
Mà AA' vuông góc BC \(\Rightarrow\overrightarrow{AA'}.\overrightarrow{BC}=0\)
\(\Rightarrow6\left(-3y-2\right)-2\left(y-4\right)=0\Rightarrow y=-\dfrac{1}{5}\)
\(\Rightarrow A'\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)


MA+MC= MA-MB
<=> 2 MI=BA
=> MI=BA/2
=> I thuộc đường tròn I bán kính AB/2
nãy mk quên giải thik:
a, gọi I la trung điểm của AC=> MA+MC=2MI
hok tốt





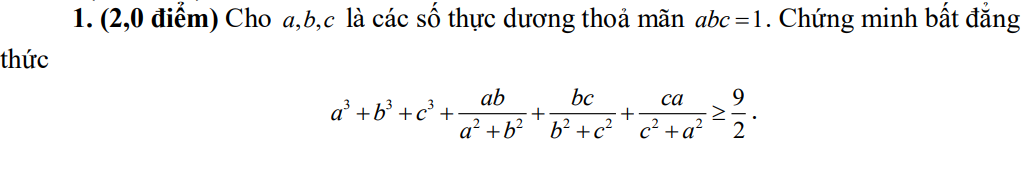 Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Hiểu như này:
\(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{b}{1+b}=3-\left(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+b}\right)\le3-\dfrac{9}{1+a+1+b+1+b}=\dfrac{3\left(a+2b\right)}{3+a+2b}\)
ghê quá :<