
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=10a\)
b: \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\dfrac{BC}{2}=5a\)

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...



Câu 1: Vì (d') vuông góc với (d) nên \(a\cdot\dfrac{-1}{3}=-1\)
hay a=3
Vậy: (d'): y=3x+b
Thay x=4 và y=-5 vào (d'), ta được:
b+12=-5
hay b=-17

3.
Do M là trung điểm BC \(\Rightarrow\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
K là trung điểm AB \(\Rightarrow\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{BA}\)
Do đó:
\(\overrightarrow{AN}+\overrightarrow{CM}-\overrightarrow{KB}=\overrightarrow{AN}+\overrightarrow{CM}+\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BA}=\overrightarrow{0}\)
4.
\(\overrightarrow{BC}=\left(6;-2\right)\)
Gọi \(A'\left(x;y\right)\Rightarrow\overrightarrow{BA'}=\left(x+3;y-1\right)\)
Do A' thuộc BC \(\Rightarrow\overrightarrow{BA'}\) và \(\overrightarrow{BC}\) cùng phương
\(\Rightarrow\dfrac{x+3}{6}=\dfrac{y-1}{-2}\Rightarrow x=-3y\)
\(\Rightarrow A'\left(-3y;y\right)\Rightarrow\overrightarrow{AA'}=\left(-3y-2;y-4\right)\)
Mà AA' vuông góc BC \(\Rightarrow\overrightarrow{AA'}.\overrightarrow{BC}=0\)
\(\Rightarrow6\left(-3y-2\right)-2\left(y-4\right)=0\Rightarrow y=-\dfrac{1}{5}\)
\(\Rightarrow A'\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)

1b)
Song song => (d): x-y +a =0
Vì d đi qua C(2;-2) => 2- (-2)+a=0
<=>a=4
=> d: x-y+4=0

Hiểu như này:
\(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{b}{1+b}=3-\left(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+b}\right)\le3-\dfrac{9}{1+a+1+b+1+b}=\dfrac{3\left(a+2b\right)}{3+a+2b}\)




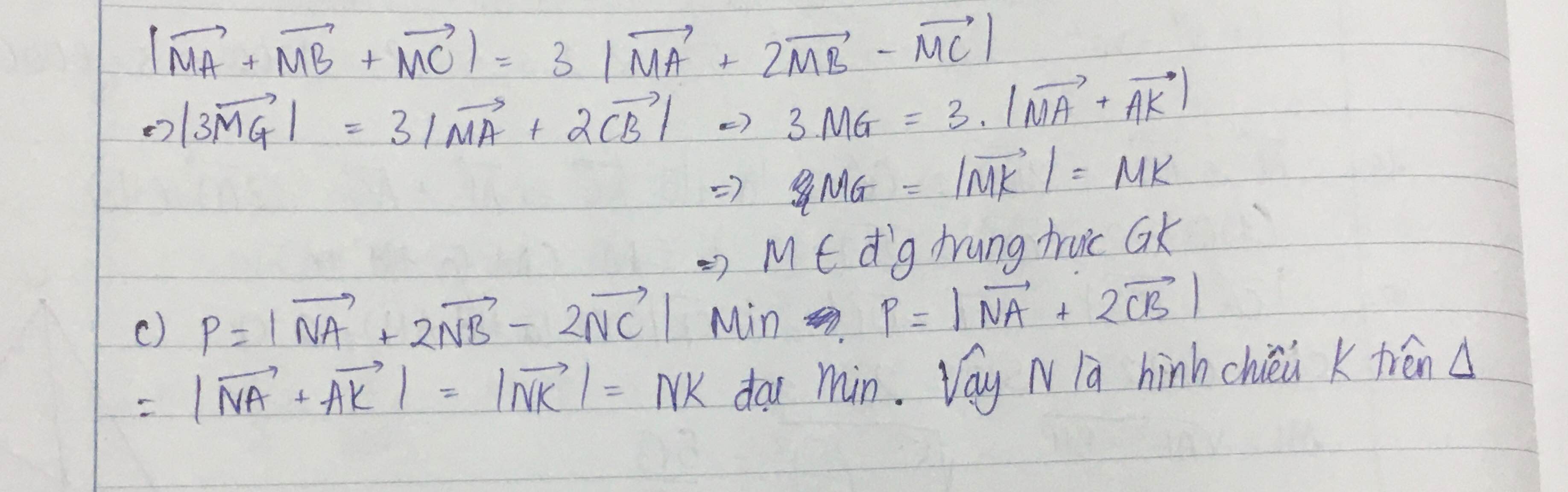 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.






.