
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


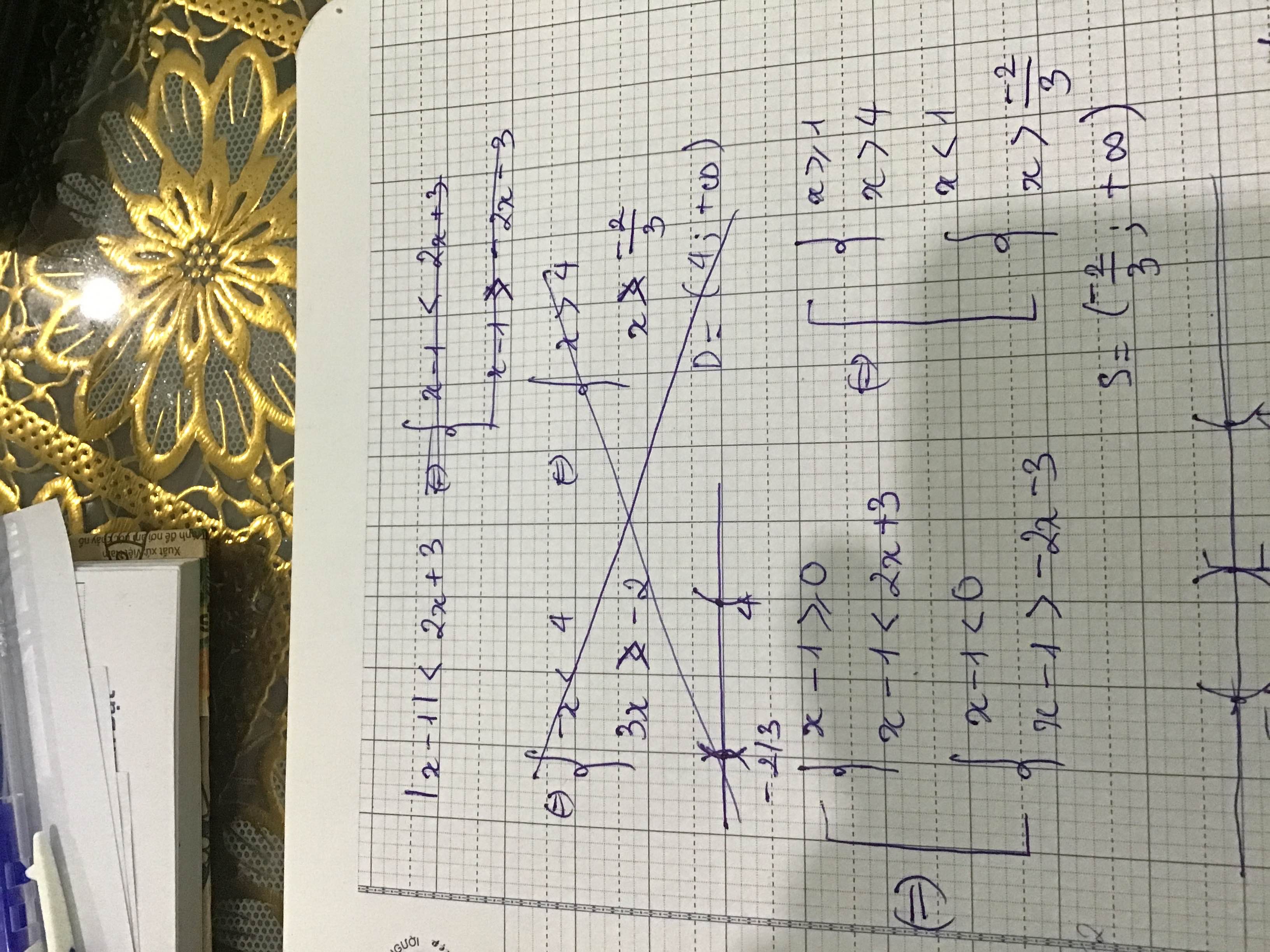
Ngoại trừ nhầm lẫn 1 chút xíu ở chỗ lẽ ra là \(x>-4\) thì em ghi thành \(x>4\), còn lại thì đúng
Kết luận nghiệm cũng đúng rồi.
Hợp nghiệm của ngoặc nhọn thì lấy giao các tập nghiệm, hợp nghiệm của ngoặc vuông thì lấy hợp các tập nghiệm

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)

cậu này muốn nói: trong cái tam giác đó M chia AB thành k lần , N chia BC thành k lần ,và P chia CÃ thành k lần . nhưng k#1 có nghĩa là chia các phần từ 2 trở nên .nếu chia một phần thì chắc chắn các cạnh của tam giác vẫn giữ nguyên.

=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ

Bài 9:
\(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}\)
\(=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{CB}\)
\(=\overrightarrow{0}\)


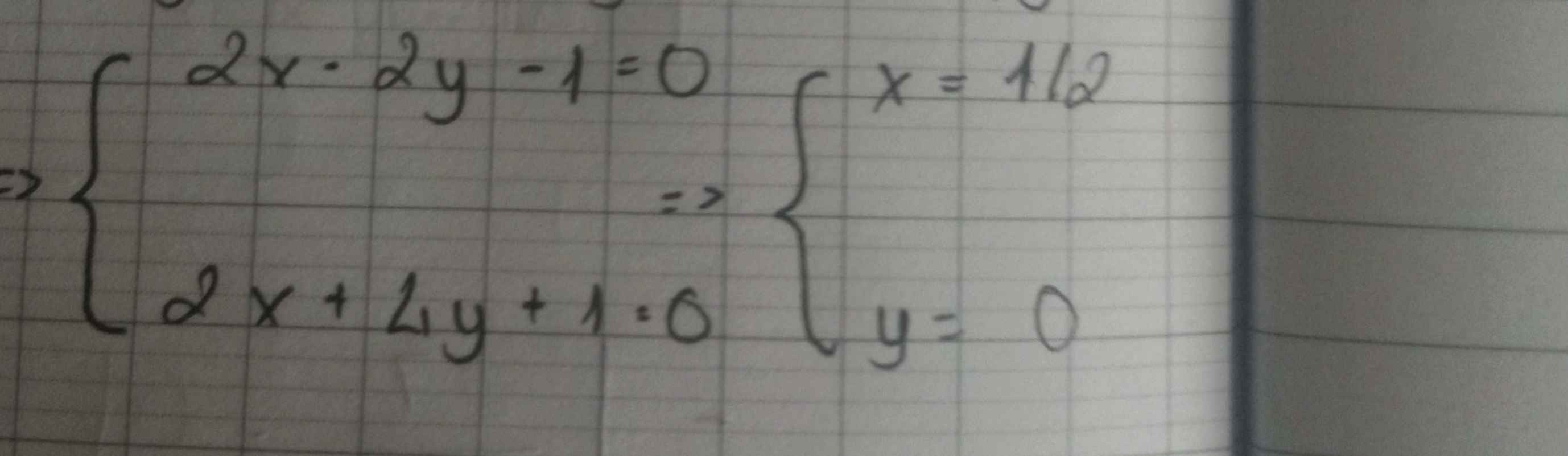
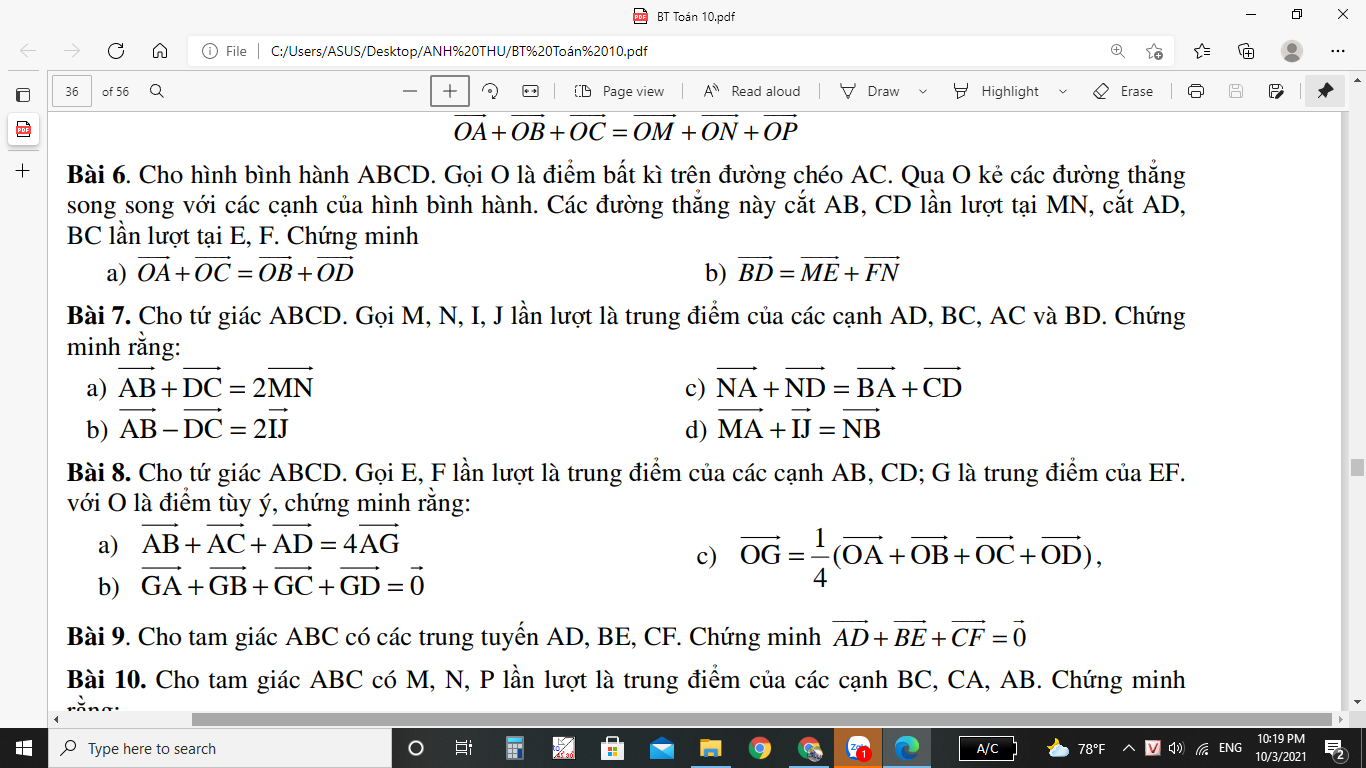 câu 8 làm thế nào vậy mn mình ko bt lm
câu 8 làm thế nào vậy mn mình ko bt lm
a: \(A\left(2;5\right);B\left(1;9\right);C\left(10;3\right)\)
\(\overrightarrow{AB}=\left(-1;4\right);\overrightarrow{AC}=\left(8;-2\right)\)
Vì \(-\dfrac{1}{8}< >\dfrac{4}{-2}\)
nên A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của một tam giác
b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=\left(-1\right)\cdot8+4\left(-2\right)=-8-8=-16< 0\)
=>ΔABC không vuông tại A
c:
\(\overrightarrow{AE}=\left(x-2;y-5\right);\overrightarrow{CB}=\left(-9;6\right)\)
AEBC là hình bình hành
=>\(\overrightarrow{AE}=\overrightarrow{CB}\)
=>\(\left\{{}\begin{matrix}x-2=-9\\y-5=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=11\end{matrix}\right.\)
Vậy: E(-7;11)