Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình có dạng \(2^{x+1}=2^{-2}\).
b) So sánh số mũ của \(2\) ở hai vế của phương trình ta được:
\(x+1=-2\Rightarrow x=-3\).

a: Sau 1 năm doanh nghiệp đó sẽ có:
\(10^9\left(1+6.2\%\right)=1062\cdot10^6\)(triệu đồng)
Sau 2 năm doanh nghiệp đo sẽ có:"
\(\left(1062\cdot10^6\right)\left(1+6.2\%\right)=1127844000\left(đồng\right)\)
Sau 3 năm doanh nghiệp đó sẽ có:
\(1127844000\left(1+6.2\%\right)=\text{1 197 770 328 }\left(đồng\right)\)
b: Công thức là: \(A=10^9\left(1+6.2\%\right)^n\)

Dân số của nước này sau 20 năm là;
\(A=19\cdot2^{\dfrac{20}{30}}\simeq30\)(triệu người)

Dân số sẽ gấp đôi dân số của năm lấy làm mốc tính:
\(S=A.e^{r.t}\Rightarrow\dfrac{1}{r}=\ln\dfrac{S}{A}\)
Do \(S_1=2S\Rightarrow t=\dfrac{1}{r}.\ln\dfrac{2S}{S}=\dfrac{1}{r}.\ln2\)

Không gian mẫu Ω = ( b , c ) : 1 ≤ b , c ≤ 6 . Kí hiệu A, B, C là các biến cố cần tìm xác suấtứng với các câu a), b), c). Ta có Δ = b 2 − 4 c
a)
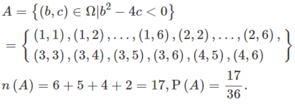
b)
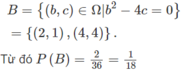
c)
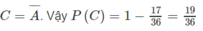

Mỗi năm số cá thể của quần thế này tăng: \(12\%-2\%-8\%=2\%\)
Giả sử số cá thể của quần thể đó là dãy số \(\left(u_n\right)\) với \(u_1=110000\)
Ta có:
\(u_1=110000\\ u_2=u_1+u_1\cdot\dfrac{2}{100}=u_1\cdot1,02\\ u_3=u_2+u_2\cdot\dfrac{2}{100}=u_2\cdot1,02\\ ...\\ u_n=u_{n-1}+u_{n-1}\cdot\dfrac{2}{100}=u_{n-1}\cdot1,02\)
Vậy số cá thể của quần thể đó tạo thành cấp số nhân với số hạng đầu \(u_1=110000\) và công bội \(q=1,02\)
Số cá thể của quần thể đó sau 2 năm là: \(u_3=u_1\cdot q^2=110000\cdot1,02^2=114444\) (cá thể)

a) Chu ký hô hấp: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{3}}} = 6\left( s \right)\)
Số chu kỳ hô hấp trong 1 phút là \(\frac{60}{6}=10\)(chu kì).
b) Ta có: \(v=0,85\sin \frac{\pi t}{3}\)
+) v > 0 khi \(0,85\sin \frac{\pi t}{3}>0\Leftrightarrow \sin \frac{\pi t}{3}>0\)
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, \(0<\sin \frac{\pi t}{3}\le 1\).
+) v < 0 khi \(0,85\sin \frac{\pi t}{3}<0\Leftrightarrow \sin \frac{\pi t}{3}<0\).
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
+) Với t ∈ (0; 3) ta có 0 < sin\(\frac{\pi t}{3}\) ≤ 1.
+) Với t ∈ (3; 5] ta có −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.

Đáp án A.
Số phần tử của không gian mẫu là ![]() Gọi A là biến cố thỏa yêu cầu bài toán.
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình ![]() có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi
![]()
Xét bảng kết quả sau (L – loại, không thỏa; N – nhận, thỏa yêu cầu đề bài):
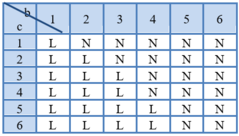
Dựa vào bảng kết quả trên ta thấy số kết quả thuận lợi cho A là 19.
Vậy xác suất của biến cố A là ![]()

Vật đi qua vị trí cân bằng thì x = 0
Khi đó
\(\begin{array}{l}2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\\Leftrightarrow t = \frac{2\pi }{15} + \frac{{k\pi }}{5} ;k \in Z\end{array}\)
Do khoảng thời gian từ 0 đến 6 giây nên \(t \in \left[ {0;6} \right]\)
\(\begin{array}{l}0 \le \ \frac{{2\pi }}{{15}} + \frac{{k\pi }}{5} \le \ 6;k \in Z\\ \Rightarrow \frac{-2 }{3}\le \ k \le \ \frac{90 - 2\pi}{3\pi};k \in Z\end{array}\)
Do \(k \in Z\) nên \(k \in \left\{ {0;1;2;3;4;5;6;7;8} \right\}\)
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.
a) Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:
\(S=2S.e^{1,14.t}\Leftrightarrow2e^{1,14t}=1\Leftrightarrow e^{1,14t}=\dfrac{1}{2}\)
b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa