Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
N x3 – 3x2 + 3x – 1 = x3 – 3.x2.1 + 3.x.12 – 13 = (x – 1)3
U 16 + 8x + x2 = 42 + 2.4.x + x2 = (4 + x)2 = (x + 4)2
H 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1 = (x + 1)3 = (1 + x)3
 1 – 2y + y2 = 12 – 2.1.y + y2 = (1 – y)2 = (y – 1)2
Điền vào bảng như sau:
| (x – 1)3 | (x + 1)3 | (y – 1)2 | (x – 1)3 | (1 + x)3 | (1 – y)2 | (x + 4)2 |
| N | H | Â | N | H | Â | U |
Vậy: Đức tính đáng quý là "NHÂN HẬU"
(Chú ý: Bạn có thể làm theo cách ngược lại, tức là khai triển các biểu thức (x – 1)3, (x + 1)3, (y – 1)2, (x + 4)2 … để tìm xem kết quả ứng với chữ nào và điền vào bảng.)

Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Nên:
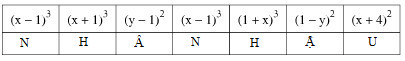
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.
Bài giải:
Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Nên:
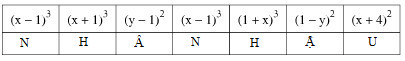
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.

a) x^3-3x^2+3x-1
=x3-3x2.1+3x.12-13
=(x-1)3
b)16+8x+x^2
=42+2.4.x+x2
=(4+x)2
c) 3x^2+3x+1+x^3
=x3+3x2.1+3x.12+13
=(x+1)3
d)1-2y+y^2
=1-2.1.y+y2
=(1-y)2

2:
-8x^6-12x^4y-6x^2y^2-y^3
=-(8x^6+12x^4y+6x^2y^2+y^3)
=-(2x^2+y)^3
3:
=(1/3)^2-(2x-y)^2
=(1/3-2x+y)(1/3+2x-y)

Bài 3:
b: Ta có: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\left(x^2-2x+1\right)+10=0\)
\(\Leftrightarrow6x^2+12-6x^2+12x-6=0\)
hay \(x=-\dfrac{1}{2}\)
Bài 2:
a: \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
b: \(m^3+9m^2n+27mn^2+27n^3=\left(m+3n\right)^3\)

1, \(x^2+2xy+y^2=\left(x+y\right)^2\)
2, \(4x^2+12x+9=\left(2x\right)^2+2\cdot3\cdot2x+3^2=\left(2x+3\right)^2\)
3, \(x^2+5x+\dfrac{25}{4}=x^2+2\cdot\dfrac{5}{2}\cdot x+\left(\dfrac{5}{2}\right)^2=\left(x+\dfrac{5}{2}\right)^2\)
4, \(16x^2-8x+1=\left(4x\right)^2-2\cdot4x\cdot1+1^2=\left(4x-1\right)^2\)
5, \(x^2+x+\dfrac{1}{4}=x^2+2\cdot\dfrac{1}{2}\cdot x+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
1: =(x+y)^2
2: =(2x+3)^2
3: =(x+5/2)^2
4: =(4x-1)^2
5: =(x+1/2)^2
6: =(x-3/2)^2
7: =(x+1)^3
8: =(1/2x+1)^2
9: =(3y-1/3)^3
10: =(2x+y)^3
\(x^3-3x^2+3x-1=\left(x-1\right)^3\)
\(x^2+8x+16=\left(x+4\right)^2\)
\(x^3+3x^2+3x+1=\left(x+1\right)^3\)
\(1-2x+x^2=\left(x-1\right)^2\)