Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương trình hoành độ giao điểm của (C) và (d) là x 3 − 3 x 2 = m ⇔ x 3 − 3 x 2 − m = 0 *
Để (C) cắt d tại 3 điểm phân biệt khi và chỉ khi (*) có 3 nghiệm phân biệt ⇔ − 4 < m < 0
Khi đó, gọi A x 1 ; m , B x 2 ; m , C x 3 ; m là giao điểm của (C) và d ⇒ A B ¯ = x 2 − x 1 ; 0 B C ¯ = x 3 − x 2 ; 0
Mà B nằm giữa A, C và A B = 2 B C suy ra A B ¯ = 2 B C ¯ ⇔ x 2 − x 1 = 2 x 3 − x 2 ⇔ x 1 + 2 x 3 = 3 x 2
Theo hệ thức Viet cho phương trình (*), ta được x 1 + x 2 + x 3 = 3 ; x 1 x 2 x 3 = m x 1 x 2 + x 2 x 3 + x 3 x 1 = 0
Giải x 1 − 3 x 2 + 2 x 3 = 0 x 1 + x 2 + x 3 = 3 x 1 x 2 + x 2 x 3 + x 3 x 1 = 0 ⇒ x 1 ; x 2 ; x 3 = 1 − 5 7 ; 1 + 1 7 ; 1 + 4 7 x 1 ; x 2 ; x 3 = 1 + 5 7 ; 1 − 1 7 ; 1 − 4 7 ⇒ m = − 98 + 20 7 49 m = − 98 − 20 7 49 ⇒ ∑ m = − 4

Chọn đáp án B.

d và (C) cắt nhau tại ba điểm phân biệt

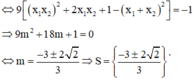
Tổng bình phương các phần tử của S là


HD: Hoành độ giao điểm của (C) và d là nghiệm phương trình:

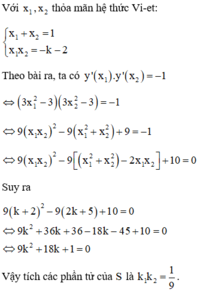
Chọn

Phương pháp:
+) Giải phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:


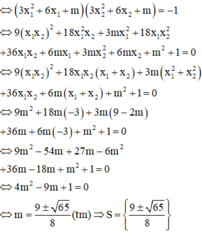
Vậy tổng các phần tử của tập hợp S bằng 9 4
Chọn: C
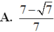


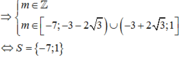

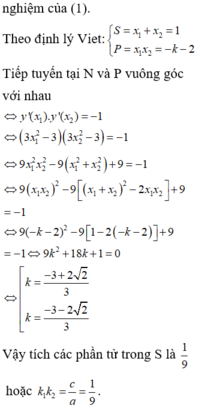
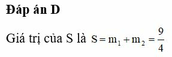





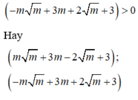
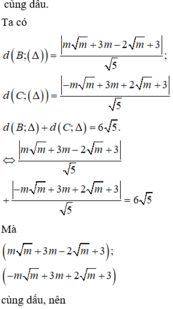

Đáp án D