K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
2
28 tháng 10 2019
\(|2x^2-3x+4|-|2x-x^2-1|=0\)
\(\Leftrightarrow|2x^2-3x+4|=|2x-x^2-1|\)
\(\Leftrightarrow\orbr{\begin{cases}2x^2-3x+4=2x-x^2-1\\2x^2-3x+4=-2x+x^2+1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x^2-3x+4-2x+x^2+1=0\\2x^2-3x+4+2x-x^2-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}3x^2-5x+5=0\\x^2-x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}3\left(x^2-\frac{5}{3}x+\frac{25}{9}-\frac{25}{9}+\frac{5}{3}\right)=0\\x^2-2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}3\left(x-\frac{5}{3}^2\right)-\frac{10}{3}=0\\\left(x-\frac{1}{2}\right)^2+\frac{11}{4}>0\left(Loai\right)\end{cases}}\)
\(\Leftrightarrow\left(x\sqrt{3}-\frac{5\sqrt{3}}{3}\right)^2-\left(\frac{\sqrt{30}}{3}\right)^2=0\)
\(\Leftrightarrow\left(x\sqrt{3}-\frac{5\sqrt{3}}{3}-\frac{\sqrt{30}}{3}\right)\left(x\sqrt{3}-\frac{5\sqrt{3}}{3}+\frac{\sqrt{30}}{3}\right)=0\)
\(\Leftrightarrow\left(x\sqrt{3}-\frac{\sqrt{30}+5\sqrt{3}}{3}\right)\left(x\sqrt{3}+\frac{\sqrt{30}-5\sqrt{3}}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x\sqrt{3}-\frac{\sqrt{30}+5\sqrt{3}}{3}=0\\x\sqrt{3}+\frac{\sqrt{30}-5\sqrt{3}}{3}=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{5+\sqrt{10}}{3}\\x=\frac{5-\sqrt{10}}{3}\end{cases}}\)
Vậy ...
C
31 tháng 10 2019
\(\left|2x^2-3x+4\right|-\left|2x-x^2-1\right|=0\)
\(\Leftrightarrow\left|2x^2-3x+4\right|=\left|2x-x^2-1\right|\)
\(\Leftrightarrow\orbr{\begin{cases}2x^2-3x+4=2x-x^2-1\\2x^2-3x+4=x^2-2x+1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}3x^2-5x+5=0\\x^2-x+3=0\end{cases}}\)
\(TH1:3x^2-5x+5=0\)
Ta có: \(\Delta=5^2-4.3.5=-35< 0\)(vô nghiệm)
\(TH2:x^2-x+3=0\)
Ta có: \(\Delta=1^2-4.1.3=-11< 0\)(vô nghiệm)
Vậy pt vô nghiệm
HP
20 tháng 11 2021
a) (P) có đỉnh I(-1; -2)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{\Delta}{4a}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2.2\\b^2-4.2.c=8.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-8c=16\end{matrix}\right.\Leftrightarrow4^2-8c=16\)
\(\Leftrightarrow c=0\)
=> y = 2x2 + 4x
b) (P) có trục đối xứng x = 1 và cắt trục tung tại M(0; 4)
\(M\in\left(P\right)\Rightarrow4=2.0^2+b.0+c\)
\(\Leftrightarrow c=4\)
Trục đối xứng: \(x=-\dfrac{b}{2a}=1\)
<=> -b = 2a
<=> -b = 2.2
<=> b = -4
=> y = 2x2 - 4x + 4
c) Đi qua 2 điểm A(1; 6), B(-1; 0)
\(A\in\left(P\right)\Rightarrow6=2.1^2+b.1+c\)
\(\Leftrightarrow b+c=4\) (1)
\(B\in\left(P\right)\Rightarrow0=2.\left(-1\right)^2+b\left(-1\right)+c\)
\(\Leftrightarrow-b+c=-2\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}b+c=4\\-b+c=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\c=1\end{matrix}\right.\)
=> y = 2x2 + 3x + 1
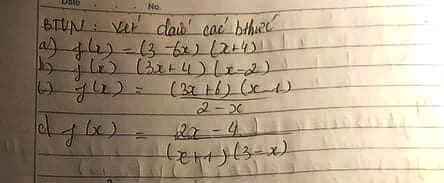
giúp mình mấy câu này với mình cảm ơn nhìu ạ
