Giúp tớ câu 44 ạ;-;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 10 2023
e: \(\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\cdot\sqrt{ab}\)
\(=a\cdot\sqrt{\dfrac{a}{b}\cdot\sqrt{ab}+2ab}+b\cdot\sqrt{\dfrac{a}{b}\cdot ab}\)
\(=a\cdot\sqrt{\dfrac{a\sqrt{ab}+2ab^2}{b}}+b\cdot a\)
\(=a\left(\sqrt{\dfrac{a\sqrt{ab}+2ab^2}{b}}+b\right)\)
\(=a\left(\dfrac{\sqrt{ab\sqrt{ab}+2ab^3}+b^2}{b}\right)\)
AT
16 tháng 7 2021
b) Từ B kẻ đường vuông góc với BC cắt AC tại E
tam giác BEC vuông tại B có \(AB=AC\Rightarrow A\) là trung điểm CE
Vì tam giác ABC cân tại A có AH là đường cao \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow AH\) là đường trung bình tam giác BEC
\(\Rightarrow AH=\dfrac{1}{2}BE\Rightarrow2AH=BE\Rightarrow4AH^2=BE^2\)
tam giác BEC vuông tại B có BK là đường cao \(\Rightarrow\dfrac{1}{BE^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
\(\Rightarrow\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
28 tháng 7 2023
a: góc BDC=180-60=120 độ
góc BOC=2*góc BAC=120 độ
góc BAD=góc CAD=60/2=30 độ
=>góc BOD=góc COD=60 độ
góc BOD=1/2*góc BOC
=>OD là phân giác của góc BOC
Xét ΔOBD có OB=OD và góc BOD=60 độ
nên ΔOBD đều
=>góc OBD=60 độ
Xét ΔOCD có OD=OC và góc DOC=60 độ
=>ΔOCD đều
=>góc OCD=60 độ
Xét tứ giác BOCD có
góc BOC=góc BDC
góc OBD=góc OCD
OB=OC
=>BOCD là hình thoi
b:
góc IBC+góc ICB=1/2(góc ABC+góc ACB)=1/2*120=60 độ
=>góc BIC=120 độ
góc BOC=góc BIC=120 độ
=>BOIC nội tiếp
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
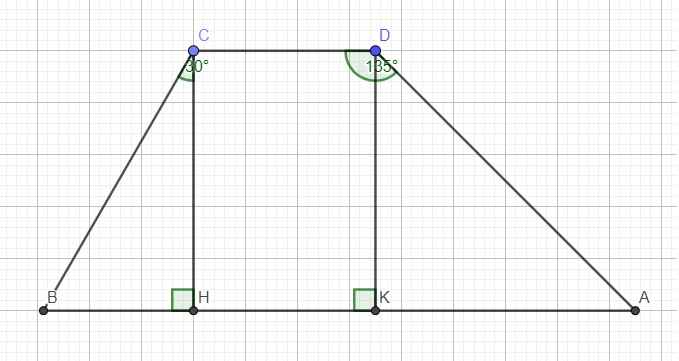
Từ D kẻ đường vuông góc DK (K thuộc AB) \(\Rightarrow CDKH\) là hình chữ nhật
\(\Rightarrow\left\{{}\begin{matrix}HK=CD=3,5\left(m\right)\\CH=DK=5\left(m\right)\end{matrix}\right.\)
Ta có:\(\widehat{KDA}=135^0-90^0=45^0\)
Trong tam giác vuông BCH:
\(cos\widehat{BCH}=\dfrac{CH}{BC}\Rightarrow BC=\dfrac{CH}{cos\widehat{BCH}}=\dfrac{5}{cos30^0}=\dfrac{10\sqrt{3}}{3}\left(m\right)\)
\(\Rightarrow BH=\sqrt{BC^2-CH^2}=\dfrac{5\sqrt{3}}{3}\left(m\right)\)
Trong tam giác vuông ADK:
\(\widehat{KAD}=90^0-\widehat{KDA}=45^0\Rightarrow\widehat{KAD}=\widehat{KDA}\Rightarrow\Delta ADK\) vuông cân tại K
\(\Rightarrow AK=DK=5\left(m\right)\)
\(\Rightarrow AD=\sqrt{AK^2+DK^2}=5\sqrt{2}\left(m\right)\)
\(AB=BH+HK+KA=\dfrac{51+10\sqrt{3}}{6}\left(m\right)\)
Chu vi: \(AB+CD+BC+AD\approx27,7\left(m\right)\)
Diện tích: \(S=\dfrac{1}{2}\left(AB+CD\right).CH\approx37,2\left(m^2\right)\)
Giải giúp tớ với ạ, tớ cần gấp lắm
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(=\left(\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(=2\sqrt{5}.\dfrac{\sqrt{2}}{\sqrt{5}}=2\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(\left(\dfrac{\sqrt{15}-\sqrt{20}}{\sqrt{3}-2}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}-\dfrac{1}{\sqrt{6}+\sqrt{5}}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{10}}{2}\)
\(=2\sqrt{5}\cdot\dfrac{2}{\sqrt{10}}=2\sqrt{2}\)
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
c.
\(\left\{\begin{matrix} 9x-6y=4\\ 15x-10y=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{6y+4}{9}\\ 15x-10y=7\end{matrix}\right.\)
\(\Rightarrow 15.\frac{6y+4}{9}-10y=7\)
\(\Leftrightarrow \frac{5}{3}(6y+4)-10y=7\Leftrightarrow \frac{20}{3}=7\) (vô lý)
Do đó hpt vô nghiệm.
d.
\(\left\{\begin{matrix} 4x+5y=3\\ x-3y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x+5y=3\\ x=3y+5\end{matrix}\right.\Rightarrow 4(3y+5)+5y=3\)
\(\Leftrightarrow 17y+20=3\Leftrightarrow 17y=-17\Leftrightarrow y=-1\)
\(x=3y+5=-3+5=2\)
Vậy HPT có nghiệm $(x,y)=(2,-1)$
Các câu còn lại bạn làm theo pp tương tự.
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
1.
HPT \(\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ 3x-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ y=3x-5\end{matrix}\right.\)
\(\Rightarrow 5x-(3x-5)=4\Leftrightarrow 2x+5=4\Leftrightarrow 2x=-1\Leftrightarrow x=\frac{-1}{2}\)
\(y=3x-5=\frac{-3}{2}-5=\frac{-13}{2}\)
Vậy HPT có nghiệm $(x,y)=(\frac{-1}{2}, \frac{-13}{2})$
44:
Xét ΔCAB và ΔCDB có
CA=CD
AB=DB
CB chung
Do đó:ΔCAB=ΔCDB
=>\(\widehat{CAB}=\widehat{CDB}=90^0\)
=>CD là tiếp tuyến của (B)