Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.


Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được


Do d' là ảnh của d qua phép tịnh tiến nên d' cùng phương d
\(\Rightarrow\) Phương trình d' có dạng: \(2x-3y+c=0\)
Gọi \(A\left(0;1\right)\) là 1 điểm thuộc d
\(T_{\overrightarrow{v}}\left(A\right)=A'\Rightarrow\left\{{}\begin{matrix}x'=0+1=1\\y'=1+\left(-2\right)=-1\end{matrix}\right.\) \(\Rightarrow A'\left(1;-1\right)\)
Thay tọa độ A' vào pt d':
\(2.1-3.\left(-1\right)+c=0\Rightarrow c=-5\)
Hay pt d' có dạng: \(2x-3y-5=0\)

Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)

a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow1+2sinx.cosx=t^2\Rightarrow2sinx.cosx=t^2-1\)
Phương trình trở thành:
\(3t=2\left(t^2-1\right)\)
\(\Leftrightarrow2t^2-3t-2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2>\sqrt{2}\left(loại\right)\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
b.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(1+\dfrac{sinx}{cosx}=2\sqrt{2}sinx\)
\(\Rightarrow sinx+cosx=2\sqrt{2}sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\)










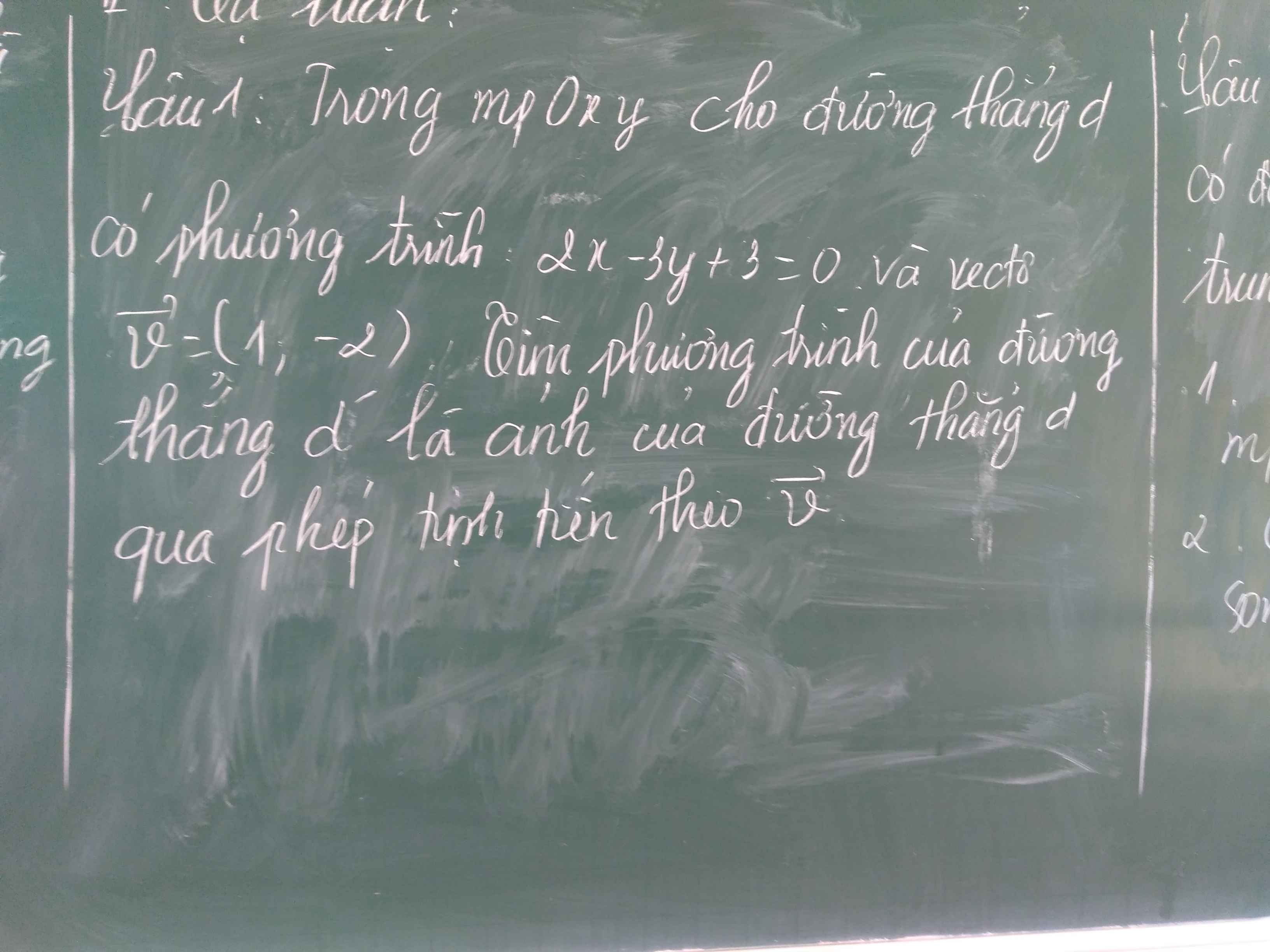



chụp rõ hơn được k bạn
đề dưới
1b
2c
3d
4a
5a
6b
7a
8d
9b
10b