TL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 9 2021
VD1 : Đề thiếu
VD2 Do a và b ∈ \(\left(0;\dfrac{\pi}{2}\right)\) nên cosa = cosb = \(\dfrac{\sqrt{3}}{2}\)
sin(a+b) = sina.cosb+cosa.sinb
cos(a - b) = cosa . cosb + sina . sinb
\(tan\left(a+b\right)=\dfrac{sin\left(a+b\right)}{cosacosb-sinasinb}\) tự thay số nhé
VD3
a, Hàm số xác định khi
\(cos\left(x-\dfrac{\pi}{4}\right)\ne0\)
⇔ \(x-\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k.\pi\)
⇔ \(x\ne\dfrac{3\pi}{4}+k.\pi\)
Tập xác định : \(D=R\backslash\left\{\dfrac{3\pi}{4}+k.\pi|k\in Z\right\}\)
b, Hàm số xác định khi sinx.cosx ≠ 0
⇔ 2sinx.cosx ≠ 0
⇔ sin2x ≠ 0
⇔ x ≠ k.π
Tập nghiệm : D = R \ {k.π | k ∈ Z}
c, D = R
d, \(sin\left(x+\dfrac{\pi}{4}\right)\ne0\Leftrightarrow x\ne-\dfrac{\pi}{4}+k.\pi\)
e, Giống câu b
PB
2
2
10 tháng 5 2023
`y'=[3(x+1)-3x-2]/[(x+1)^2]=1/[(x+1)^2]`
Gọi `M(x_0; y_0)-` tiếp điểm
Mà `y_0=[3x_0+2]/[x_0+1] in T T`
`=>y-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`@` Gọi `T T nn Ox =A`
`=>-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`<=>(-3x_0 -2)(x_0+1)=x-x_0`
`<=>-3x_0 ^2-3x_0 -2x_0 -2=x-x_0`
`<=>x=-3x_0 ^2-4x_0 -2`
`=>OA=|-3x_0 ^2-4x_0 -2|`
`@` Gọi `T T nn Oy=B`
`=>y-[3x_0 +2]/[x_0 +1]=1/[(x_0 +1)^2](-x_0)`
`<=>y=[(3x_0+2)(x_0+1)-x_0]/[(x_0+1)^2]`
`<=>y=[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]`
`=>OB=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
Vì `\triangle OAB` vuông cân tại `O`
`=>OA=OB`
`<=>|-3x_0 ^2-4x_0 -2|=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
`<=>(x_0+1)^2=1`
`<=>[(x_0=0),(x_0=-2):}`
`=>` PTTT: `[(y=x+2),(y=x+6):}`
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2022
Trong mp (ABCD) từ A kẻ \(AE\perp BD\), trong mp (SAE) từ A kẻ \(AF\perp SE\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AE\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAE\right)\)
\(\Rightarrow BD\perp AF\) (2)
(1);(2) \(\Rightarrow AF\perp\left(SBD\right)\Rightarrow AF=d\left(A;\left(SBD\right)\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
37.
\(\overrightarrow{MO}=\overrightarrow{MA}+\overrightarrow{AO}=\dfrac{1}{2}\overrightarrow{A'A}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{1}{2}\overrightarrow{B'B}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\)
\(=\dfrac{1}{2}\overrightarrow{B'C}+\dfrac{1}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{MO};\overrightarrow{AB};\overrightarrow{B'C}\) đồng phẳng
38. A đúng (B chỉ dành cho 2 đường thẳng chéo nhau)
39. A là khẳng định sai (nếu a;b cùng thuộc mặt phẳng (P) và c vuông góc (P) thì c luôn vuông góc cả a và b, bất chấp a và b có vị trí như thế nào)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
\(4sin^2x-2\left(\sqrt{3}+\sqrt{2}\right)sinx+\sqrt{6}=0\)
\(\Leftrightarrow4sin^2x-2\sqrt{3}sinx-2\sqrt{2}sinx+\sqrt{6}=0\)
\(\Leftrightarrow2sinx\left(2sinx-\sqrt{3}\right)-\sqrt{2}\left(2sinx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left(2sinx-\sqrt{3}\right)\left(2sinx-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{\sqrt{3}}{2}\\sinx=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
20 tháng 6 2019
\(\orbr{\begin{cases}2x+\frac{\pi}{6}=x+k2\pi\\2x+\frac{\pi}{6}=\pi-x+k2\pi\end{cases}}\) \(\Rightarrow\orbr{\begin{cases}x=-\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{18}+\frac{k2\pi}{3}\end{cases}}\)
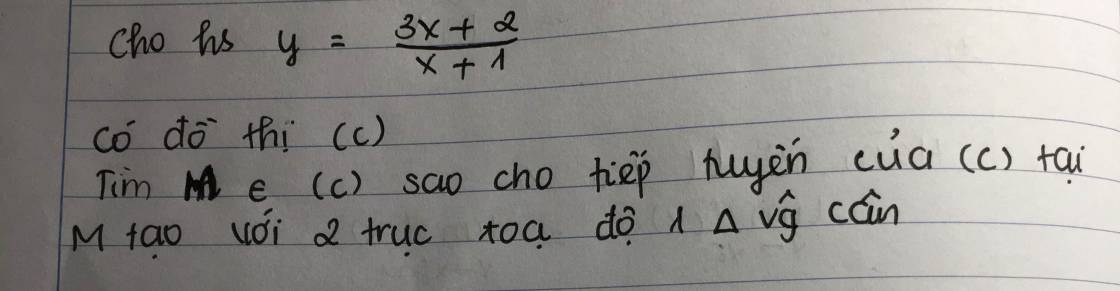
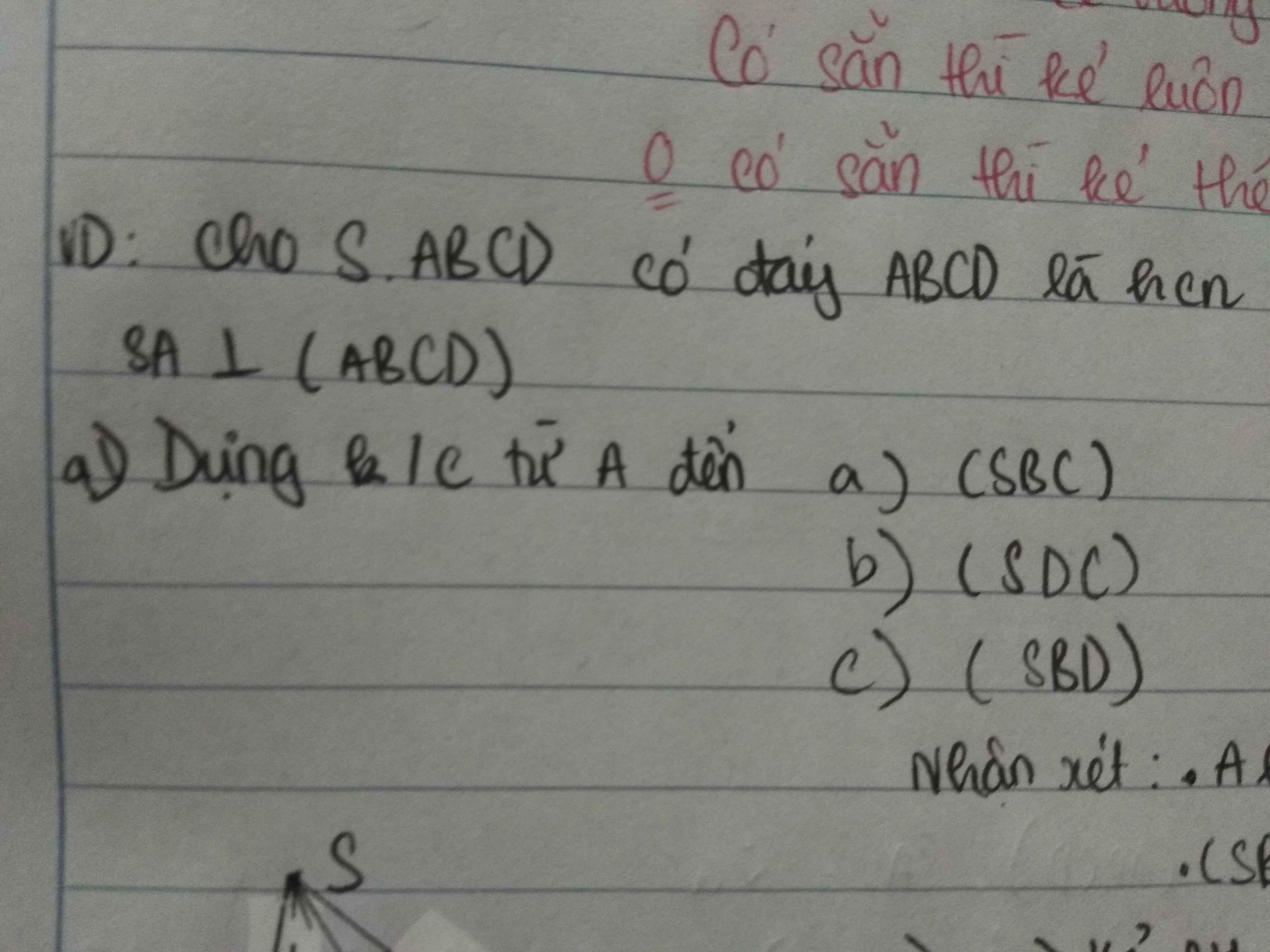
Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.
c