
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


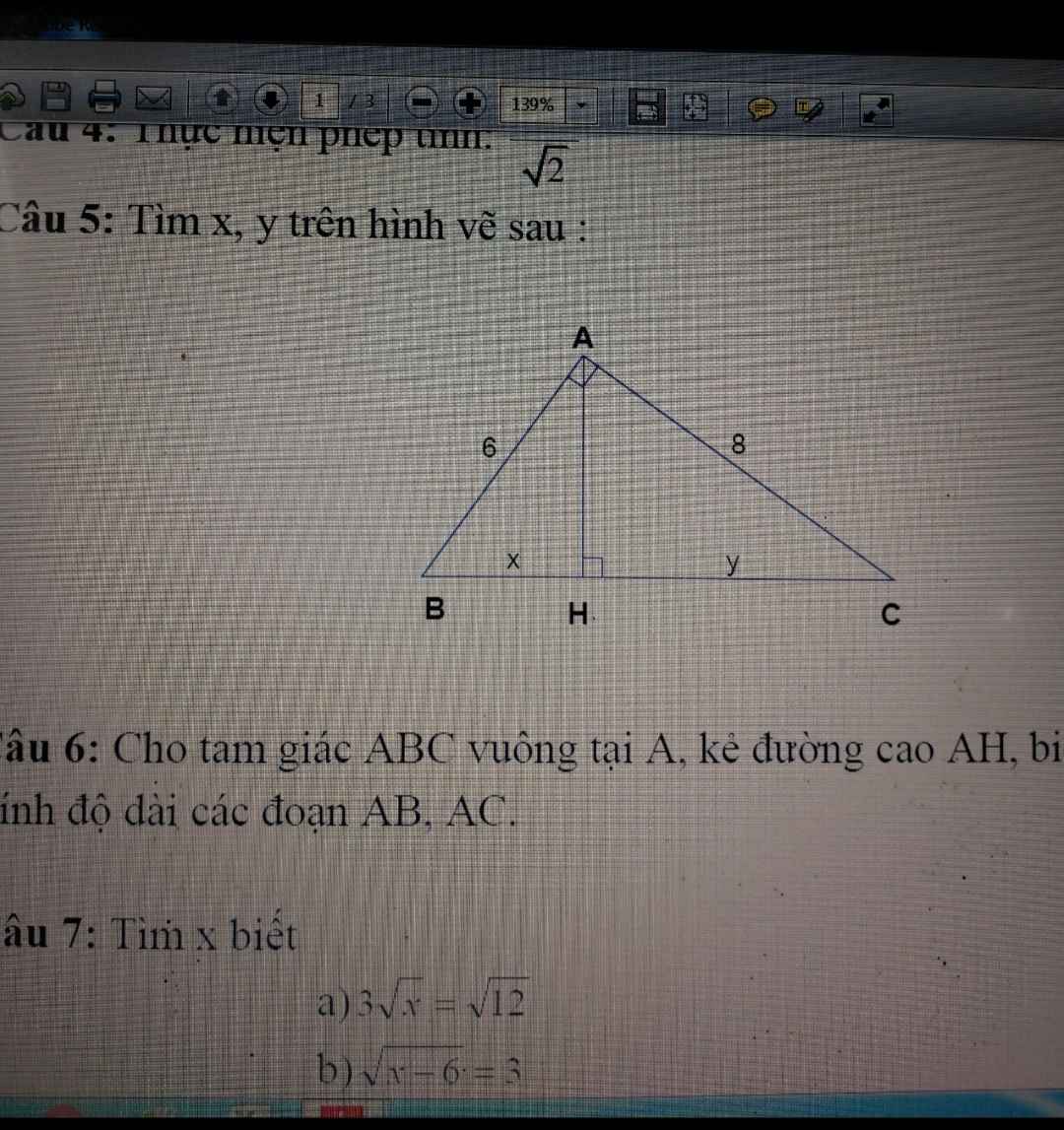
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)

Câu 1:
Ta có 2x - y = 8 => 2x - y + 9 = 17
Mà 3x + y = 17 => 2x - y + 9 = 3x + y
<=> 9 - y = x + y <=> 9 = x + 2y <=> x = 9 - 2y
Mà 2x - y = 8 => 18 - 4y - y = 8 => 18 - 5y = 8 => y = 2 => x = 5

\(a,P=\dfrac{3\sqrt{a}-3}{\sqrt{a}\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}-1}\left(a\ge0;a\ne1\right)\\ P=\dfrac{3\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}=\dfrac{3\left(\sqrt{a}+1\right)}{\sqrt{a}}\\ b,a=4\Leftrightarrow\sqrt{a}=2\\ \Leftrightarrow P=\dfrac{3\left(2+1\right)}{2}=\dfrac{9}{2}\)

Câu 20: Giao điểm của đồ thị và trục tung là điểm có toạ độ (0;-3)
Thay ngược vào phương trình => b = -3. Vậy chọn D






Câu 3:
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)