giúp em với ạ, em đang vội mong mn giúp đỡ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
3
21 tháng 10 2021
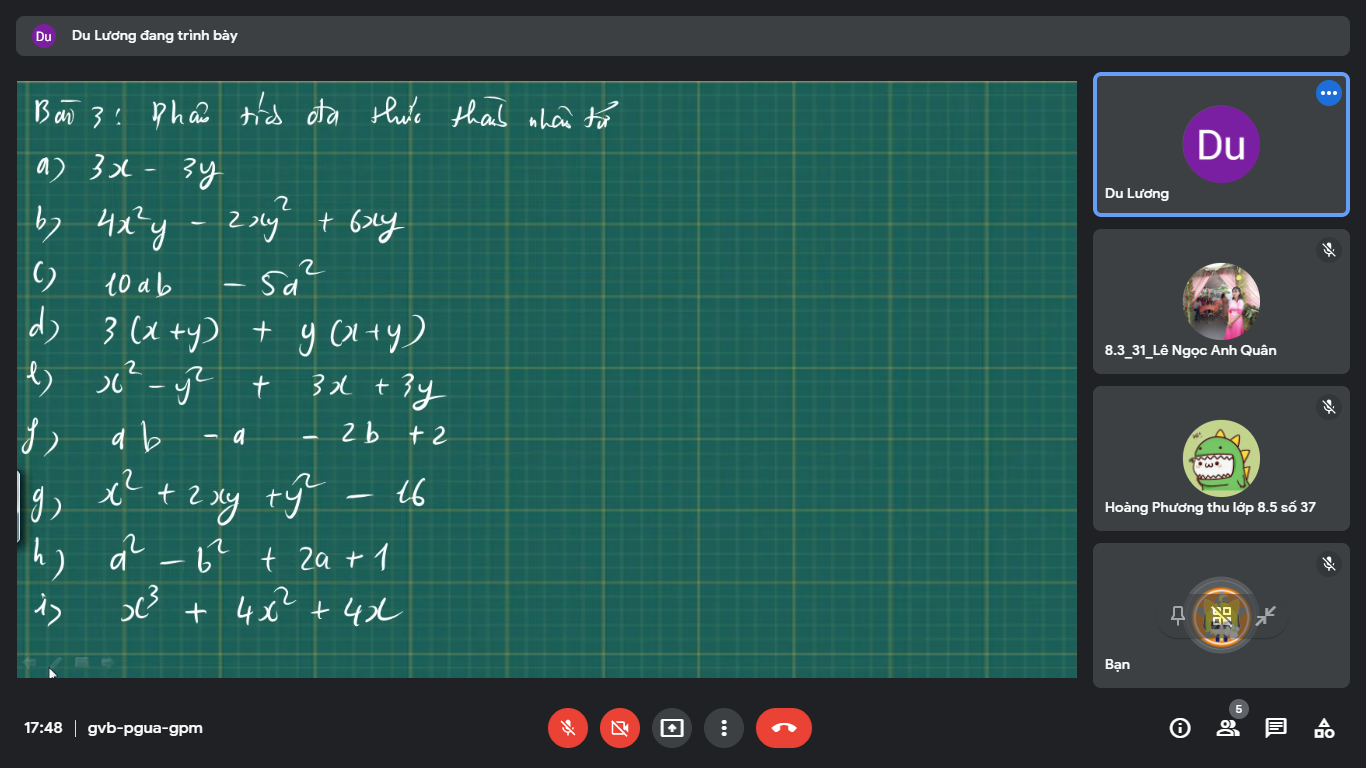
Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
TN
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
1
5 tháng 8 2021
Bài 3:
2) Ta có: \(B=2x\left(y-z\right)+\left(z-y\right)\left(x+t\right)\)
\(=2x\left(y-z\right)-\left(x+t\right)\left(y-z\right)\)
\(=\left(y-z\right)\left(x-t\right)\)
\(=\left(24-10,6\right)\left(18,3+31,7\right)\)
\(=13,4\cdot50=670\)
3) Ta có: \(C=\left(x-y\right)\left(y+z\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(y+z\right)-y\left(x-y\right)\)
\(=z\left(x-y\right)\)
\(=1.5\left(0.86-0.26\right)\)
\(=0,9\)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Lời giải:
a.
$A=\frac{3x+15}{(x-3)(x+3)}+\frac{x-3}{(x+3)(x-3)}-\frac{2(x+3)}{(x-3)(x+3)}$
$=\frac{3x+15+(x-3)-2(x+3)}{(x+3)(x-3)}=\frac{2x+6}{(x-3)(x+3)}$
$=\frac{2(x+3)}{(x-3)(x+3)}=\frac{2}{x-3}$
b.
Để $A=\frac{1}{2}$
$\Leftrightarrow \frac{2}{x-3}=\frac{1}{2}$
$\Leftrightarrow x-3=4$
$\Leftrightarrow x=7$ (tm)
10 tháng 12 2021
\(a,3x-3y=3\left(x-y\right)\\ b,4x^2y-2xy^2+6xy=2xy\left(2x-y+3\right)\\ c,10ab-5a^2=5a\left(2b-a\right)\\ d,3\left(x+y\right)+y\left(x+y\right)=\left(x+y\right)\left(3+y\right)\\ e,x^2-y^2+3x+3y=\left(x-y\right)\left(x+y\right)+3\left(x+y\right)=\left(x+y\right)\left(x-y+3\right)\\ f,ab-a-2b+2=a\left(b-1\right)-2\left(b-1\right)=\left(a-2\right)\left(b-1\right)\)
\(g,x^2+2xy+y^2-16=\left(x+y\right)^2-4^2=\left(x+y+4\right)\left(x+y-4\right)\\ h,a^2-b^2+2a+1=\left(a^2+2a+1\right)-b^2=\left(a+1\right)^2-b^2=\left(a+b+1\right)\left(a-b+1\right)\\ i,x^3+4x^2+4=x\left(x^2+4x+4\right)=x\left(x+2\right)^2\)
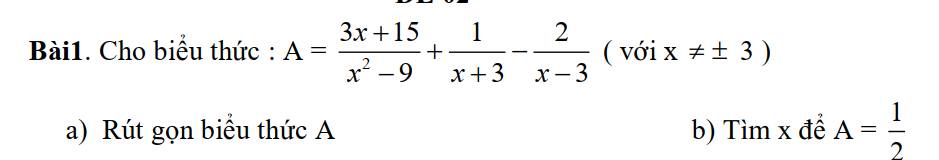
a: Xét ΔABC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}\)
hay DM=3,5(cm)