giúp e với mng ơi. e cảm ơn 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
1 tháng 5 2023
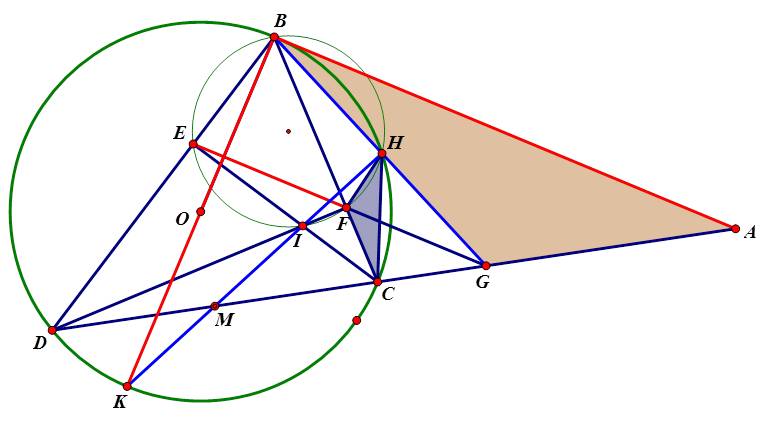
Từ điểm A nằm ngoài đường tròn (O; R) với OA > 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC < AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD.
a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.
b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GAB
c) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với CD
TH
1
28 tháng 2 2022
Câu 1:
Gọi chiều rộng là x
Chiều dài là x+20
Theo đề, ta có: 2(x+x+20)=104
=>2x+20=52
=>2x=32
hay x=16
Vậy: Diện tích của miếng đất là 16x36=576(m2)
28 tháng 2 2022
Xin lỗi nhưng e cần bài này dạng Giải bài bằng cách lập hệ phương trình ạ
5 tháng 11 2021
Bài 1:
a: \(=\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)=2\)
b: \(=\sqrt{11}+\sqrt{2}-\sqrt{11}-\sqrt{7}-\sqrt{2}=-\sqrt{7}\)
LB
0
PM
0
LK
0
R
0
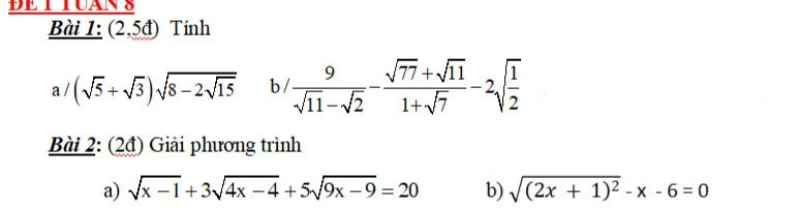
\(x^3=8+3\sqrt[3]{\left(4-2\sqrt[]{2}\right)\left(4+2\sqrt[]{2}\right)}\left(\sqrt[3]{4-2\sqrt[]{2}}+\sqrt[]{4+2\sqrt[]{2}}\right)\)
\(\Rightarrow x^3=8+6x\)
\(\Rightarrow x^3-6x=8\)
Do đó:
\(P=x\left(x^3-6x\right)-8x+24=8x-8x+24=24\)