K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 8 2021
Bài 2:
a:\(18a^2b-54a^2b^2+72ab\)
\(=18ab\left(a-3ab+4\right)\)
b: \(7a-b^2+7b-ab\)
\(=7\left(a+b\right)-b\left(a+b\right)\)
\(=\left(a+b\right)\left(7-b\right)\)
c: \(a^2-9b^2-6a+9\)
\(=\left(a-3\right)^2-9b^2\)
\(=\left(a-3-3b\right)\left(a-3+3b\right)\)
Bài 4:
Ta có: \(X=a^3-3a^2+3a\)
\(=a^3-3a^2+3a-1+1\)
\(=\left(a-1\right)^3+1\)
\(=100^3+1=1000001\)
15 tháng 8 2021
Bài 3:
a: Ta có: \(5a\left(5a-1\right)-\left(5a+1\right)\left(5a-1\right)=8\)
\(\Leftrightarrow25a^2-5a-25a^2+1=8\)
\(\Leftrightarrow5a=-7\)
hay \(a=-\dfrac{7}{5}\)
b: Ta có: \(a^2-3a+9-3a=0\)
\(\Leftrightarrow a\left(a-3\right)-3\left(a-3\right)=0\)
\(\Leftrightarrow\left(a-3\right)^2=0\)
\(\Leftrightarrow a-3=0\)
hay a=3
11 tháng 9 2021
Ta có: \(\left(x^{3n}+y^{3n}\right)\left(x^{3n}-y^{3n}\right)=-x^{6n}-y^{6n}\)
\(\Leftrightarrow x^{6n}-y^{6n}=-x^{6n}-y^{6n}\)
\(\Leftrightarrow n\in\varnothing\)
12 tháng 3 2022
Sửa đề: \(\dfrac{7}{x+5}-\dfrac{x}{5-x}=\dfrac{-x^2}{25-x^2}\)
\(\Leftrightarrow7\left(x-5\right)+x\left(x+5\right)=x^2\)
\(\Leftrightarrow7x-35+5x=0\)
=>12x=35
hay x=35/12
BB
0
30 tháng 3 2022
e: 7x<=9x-5
=>7x-9x<=-5
=>-2x<=-5
=>x>=5/2
f: \(\Leftrightarrow7x-5< 8\left(3x-1\right)-4\left(2x+4\right)\)
=>7x-5<24x-8-8x-16
=>7x-5<16x-24
=>-9x<-19
hay x>19/9
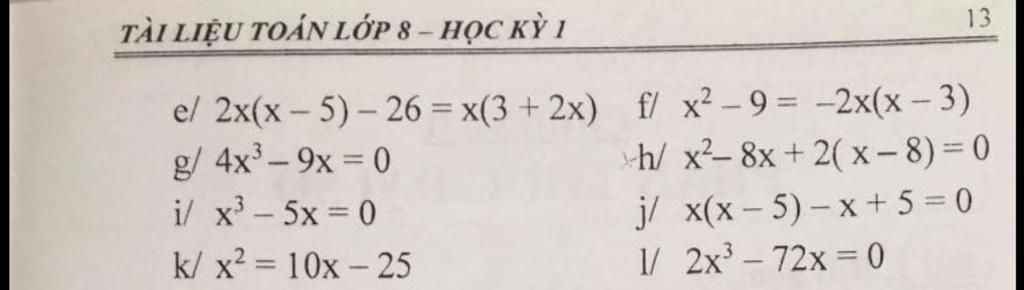
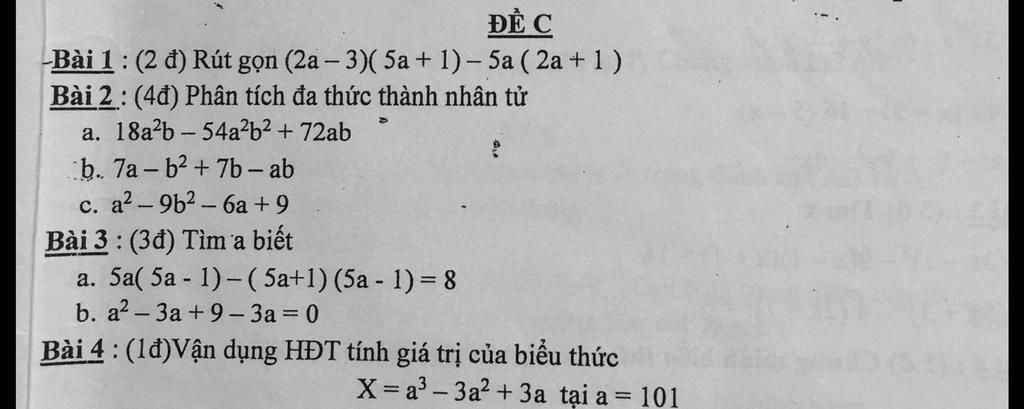
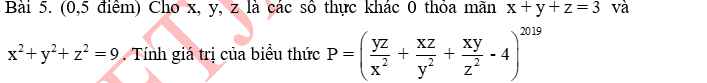
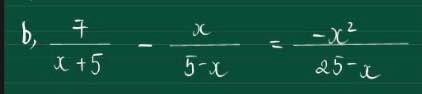
e: Ta có: \(2x\left(x-5\right)-26=x\left(2x+3\right)\)
\(\Leftrightarrow2x^2-10x-26-2x^2-3x=0\)
\(\Leftrightarrow-13x=26\)
hay x=-2
f: Ta có: \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)+2x\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
g: Ta có: \(4x^3-9x=0\)
\(\Leftrightarrow x\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
h: Ta có: \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
e. \(2x\left(x-5\right)-26=x\left(3+2x\right)\)
\(\Leftrightarrow2x^2-10x-26=3x+2x^2\)
\(\Leftrightarrow2x^2-10x-3x-2x^2=26\)
\(\Leftrightarrow-13x=26\) \(\Leftrightarrow x=-2\)
g. \(4x^3-9x=0\)
\(\Leftrightarrow x\left(4x^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x^2-9=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{9}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\dfrac{3}{2}\end{matrix}\right.\)
i. \(x^3-5x=0\)
\(\Leftrightarrow x\left(x^2-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{5}\end{matrix}\right.\)
k. \(x^2=10x-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
f. \(x^2-9=-2x\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=-2x\left(x-3\right)\)
\(\Leftrightarrow x+3=-2x\)
\(\Leftrightarrow3x=-3\)
\(\Leftrightarrow x=-1\)
h. \(x^2-8x+2\left(x-8\right)=0\)
\(\Leftrightarrow x\left(x-8\right)+2\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
j. \(x\left(x-5\right)-x+5=0\)
\(\Leftrightarrow x\left(x-5\right)-\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
l. \(2x^3-72x=0\)
\(\Leftrightarrow2x\left(x^2-36\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-36=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=36\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm6\end{matrix}\right.\)