K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
\(y=13\left(x^{13}+1\right)^2=13\left(x^{26}+2x^{13}+1\right)\)
\(\Rightarrow y'=13\left(26x^{25}+26x^{12}\right)\)
\(\Rightarrow y'\left(1\right)=13\left(26+26\right)=676\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
Đáy là bát giác đều (8 cạnh) nên chóp có 8 mặt bên
Cộng thêm mặt đáy nữa nên ta sẽ có tổng cộng 9 mặt
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
6.
SAB cân tại S \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Hay SH alf đường cao của chóp
NT
6
HP
20 tháng 9 2021
3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
HP
20 tháng 9 2021
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)
KB
3 tháng 5 2022
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)
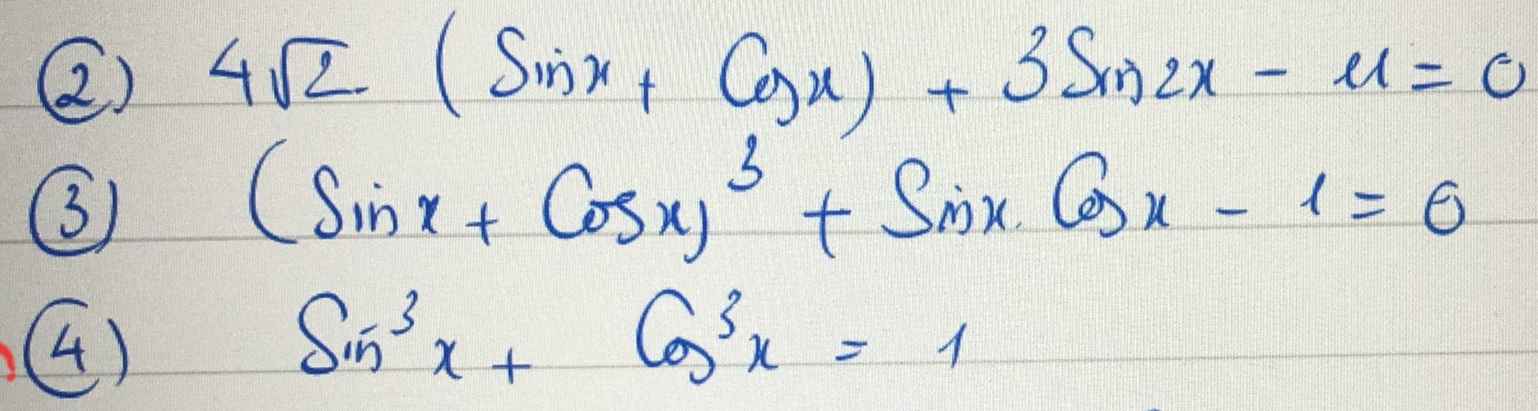
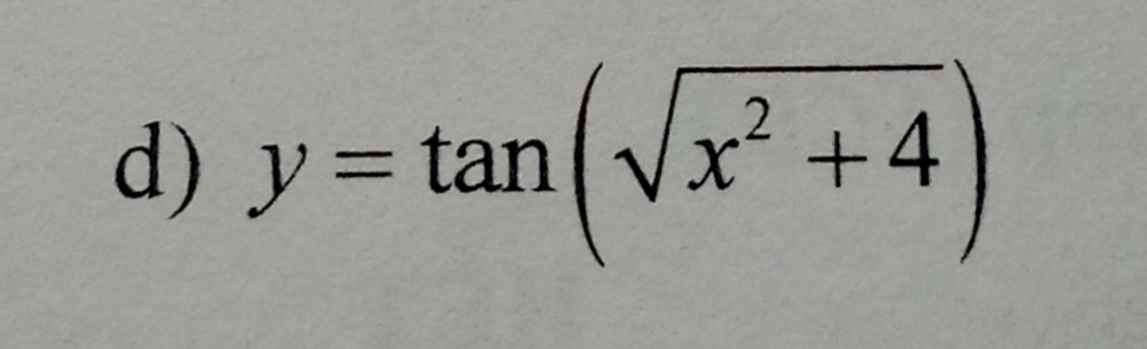
Qua S kẻ đường thẳng d song song BC \(\Rightarrow s=\left(SBC\right)\cap\left(SAD\right)\)
Nối PM kéo dài cắt d tại Q \(\Rightarrow Q\in\left(SAD\right)\)
Trong mp (SAD), nối QN cắt SA tại E và AD tại F
\(\Rightarrow E=SA\cap\left(MNP\right)\)
Do \(SQ||BC\) , theo Talet: \(\dfrac{SQ}{BP}=\dfrac{SM}{BM}=1\Rightarrow SQ=BP=\dfrac{1}{2}BC=\dfrac{1}{2}AD\)
Do \(SQ||AD\Rightarrow\dfrac{SQ}{DF}=\dfrac{SN}{ND}=1\Rightarrow DF=SQ=\dfrac{1}{2}AD\)
\(\Rightarrow AF=AD+DF=\dfrac{3}{2}AD\)
\(\Rightarrow\dfrac{SE}{AE}=\dfrac{SQ}{AF}=\dfrac{\dfrac{1}{2}AD}{\dfrac{3}{2}AD}=\dfrac{1}{3}\Rightarrow SE=\dfrac{1}{3}AE\)
\(\Rightarrow\dfrac{SE}{SA}=\dfrac{1}{4}\)