
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt[n]{y}=4x+1\)
\(y^{\dfrac{1}{n}}=4x+1\)
đạo cấp 1
\(\dfrac{1}{n}y^{\left(\dfrac{1}{n}-1\right)}=\dfrac{1}{n}\sqrt[n]{y^{\left(1-n\right)}}=4\)
thay y=(4x+1)^n vào
\(\dfrac{1}{n}\sqrt[n]{\left(4x+1\right)^{n\left(1-n\right)}}=\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}\)
từ đó: \(y'=\dfrac{4}{\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}}=4.n\left(4x+1\right)^{n-1}\)
Có đúng không: cấp n có thể phải làm lấy vài cái--> quy luật nào đó

c.
\(y'=\dfrac{\left(2x-1\right)'\left(4x-3\right)-\left(4x-3\right)'\left(2x-1\right)}{\left(4x-3\right)^2}=\dfrac{2\left(4x-3\right)-4\left(2x-1\right)}{\left(4x-3\right)^2}\)
\(=\dfrac{-2}{\left(4x-3\right)^2}\)
d.
\(y'=-\dfrac{3.\left(2x+1\right)'}{\left(2x+1\right)^2}=-\dfrac{6}{\left(2x+1\right)^2}\)

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.

1.
\(y'=\left(cos^2\left(2x+3\right)\right)'=2cos\left(2x+3\right).\left(cos\left(2x+3\right)\right)'\)
\(=2cos\left(2x+3\right).\left(-sin\left(2x+3\right)\right).\left(2x+3\right)'\)
\(=-4sin\left(2x+3\right).cos\left(2x+3\right)\)
\(=-4sin\left(4x+6\right)\)
2.
\(f'\left(x\right)=-x^2+\left(3m-2\right)x-\left(2m^2-5m-2\right)\)
Để \(f'\left(x\right)< 0;\forall x\in R\)
\(\Leftrightarrow\Delta=\left(3m-2\right)^2-4\left(2m^2-5m-2\right)< 0\)
\(\Leftrightarrow m^2+8m+12< 0\)
\(\Rightarrow-6< m< -2\)

6.
SAB cân tại S \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Hay SH alf đường cao của chóp

7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)

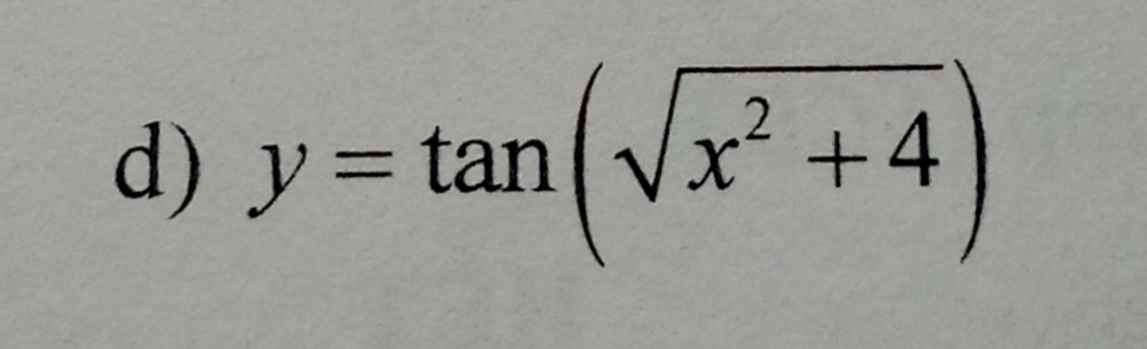








\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)