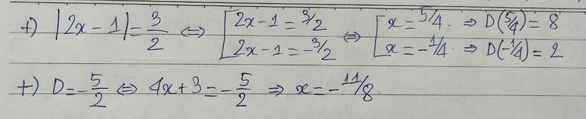Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x-1}{65}+\dfrac{x-3}{63}=\dfrac{x-5}{61}+\dfrac{x-7}{59}\)
\(\Leftrightarrow\dfrac{x-1}{65}-1+\dfrac{x-3}{63}-1=\dfrac{x-5}{61}-1+\dfrac{x-7}{59}-1\)
\(\Leftrightarrow\dfrac{x-66}{65}+\dfrac{x-66}{63}=\dfrac{x-66}{61}+\dfrac{x-66}{59}\)
\(\Leftrightarrow\left(x-66\right)\left(\dfrac{1}{65}+\dfrac{1}{63}-\dfrac{1}{61}-\dfrac{1}{59}\right)=0\)
\(\Leftrightarrow x-66=0\)
\(\Leftrightarrow x=66\)
Vậy x=66.

A = \(\dfrac{22-3x}{4-x}\)
A = \(\dfrac{3.\left(4-x\right)+10}{4-x}\)
A = 3 + \(\dfrac{10}{4-x}\)
A lớn nhất khi \(\dfrac{10}{4-x}\) lớn nhất. Vì 10 > 0; \(x\) \(\in\) Z nên \(\dfrac{10}{4-x}\) lớn nhất khi
4 - \(x\) = 1 ⇒ \(x\) = 4 - 1 ⇒ \(x\) = 3
Vậy Amin = 3 + \(\dfrac{10}{1}\) = 13 khi \(x\) =3
Kết luận giái trị lớn nhất của biểu thức là 13 xảy ra khi \(x\) = 3

a, Theo đề ta có:
\(2.3^x-405=3^{x-1}\)
=> \(2.3^x-405=3^x:3\)
=> \(405=(2.3^x)-(3^x:3)\)
=>\(405=(2.3^x)-(3^x.\dfrac{1}{3})\)
=> \(405=3^x(2-\dfrac{1}{3})\)
=>\(405=3^x(\dfrac{6}{3}-\dfrac{1}{3})\)
=> \(405=3^x.\dfrac{5}{3}\)
=> \(3^x=405:\dfrac{5}{3}\)
=>\(3^x=405.\dfrac{3}{5}\)
=> \(3^x=81.3\)
=> \(3^x=243\)
=> \(3^x=3^5\)
=> x=5
Vậy:..............................

\(\dfrac{x+35}{65}+\dfrac{x+39}{61}=\dfrac{x+43}{57}+\dfrac{x+47}{53}\)
\(\Leftrightarrow\dfrac{x+35}{65}+1+\dfrac{x+39}{61}+1=\dfrac{x+43}{57}+1+\dfrac{x+47}{53}+1\)
\(\Leftrightarrow\dfrac{x+100}{65}+\dfrac{x+100}{61}-\dfrac{x+100}{57}-\dfrac{x+100}{53}=0\)
\(\Leftrightarrow\left(x+100\right)\left(\dfrac{1}{65}+\dfrac{1}{61}-\dfrac{1}{57}-\dfrac{1}{53}\ne0\right)=0\Leftrightarrow x=-100\)
Ta có:
\(\dfrac{x+35}{65}+\dfrac{x+39}{61}=\dfrac{x+43}{57}+\dfrac{x+47}{53}\\ \Rightarrow\left(\dfrac{x+35}{65}+1\right)+\left(\dfrac{x+39}{61}+1\right)=\left(\dfrac{x+43}{57}+1\right)+\left(\dfrac{x+47}{53}+1\right)\\ \Rightarrow\dfrac{x+100}{53}+\dfrac{x+100}{61}=\dfrac{x+100}{57}+\dfrac{x+100}{53}\\ \Rightarrow\left(x+100\right)\left(\dfrac{1}{65}+\dfrac{1}{61}-\dfrac{1}{57}-\dfrac{1}{53}\right)=0\)
Ta thấy:
\(\dfrac{1}{65}< \dfrac{1}{57}\\ \dfrac{1}{61}< \dfrac{1}{53}\\ \Rightarrow\left(\dfrac{1}{65}+\dfrac{1}{62}\right)-\left(\dfrac{1}{57}+\dfrac{1}{53}\right)< 0\)
Hay \(\dfrac{1}{65}+\dfrac{1}{62}-\dfrac{1}{57}-\dfrac{1}{53}\ne0\)
\(\Rightarrow x+100=0\\ \Rightarrow x=0-100\\ \Rightarrow x=-100\)
Vậy \(x=-100\)

\(\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\left(0,5-1\dfrac{3}{5}\right)\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\left(\dfrac{1}{2}-\dfrac{8}{5}\right)\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\dfrac{11}{10}\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{33}{80}\)
\(\Rightarrow x:2,2=\dfrac{33}{80}:\dfrac{1}{6}\)
\(\Rightarrow x:2,2=\dfrac{99}{40}\)
\(\Rightarrow x=\dfrac{99}{40}\times2,2\)
\(\Rightarrow x=\dfrac{1089}{200}\)
=>(x:2,2)*1/6=-3/8(1/2-8/5)=33/80
=>x:2,2=99/40
=>x=1089/200

\(3,=\left(\dfrac{13}{25}-\dfrac{38}{25}\right)+\left(\dfrac{14}{9}-\dfrac{5}{9}\right)=-1+1=0\\ 4,=\left(\dfrac{4}{9}\right)^5\cdot\left(\dfrac{9}{49}\right)^5=\left(\dfrac{4}{9}\cdot\dfrac{9}{49}\right)^5=\left(\dfrac{4}{49}\right)^5\\ 5,\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x-y}{5-3}=\dfrac{x+y}{5+3}=\dfrac{2}{2}=\dfrac{x+y}{8}\Rightarrow x+y=8\\ 6,\Rightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\Rightarrow2\text{ giá trị}\\ 7,=\dfrac{3^{10}\cdot2^{30}}{2^9\cdot3^9\cdot2^{20}}=2\cdot3=6\)

\(\left|2x-1\right|=\dfrac{3}{2}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{3}{2}\\2x-1=-\dfrac{3}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Thay \(x=\dfrac{5}{4}\) vào D ta có:
\(D=4x+3=4.\dfrac{5}{4}+3=5+3=8\)
Thay \(x=-\dfrac{1}{4}\) vào D ta có:
\(D=4.\dfrac{-1}{4}+3=-1+3=2\)
Để \(D=\dfrac{3}{2}\)
\(\Leftrightarrow4x+3=\dfrac{3}{2}\\ \Leftrightarrow4x=-\dfrac{3}{2}\\ \Leftrightarrow x=-\dfrac{3}{8}\)

a: Ta có: \(\dfrac{x+1}{2}=\dfrac{2}{x+1}\)
\(\Leftrightarrow\left(x+1\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
b: Ta có: \(\dfrac{\left(x-2\right)^2}{7}=\dfrac{49}{\left(x-2\right)}\)
\(\Leftrightarrow x-2=7\)
hay x=9