Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{{21}}{{13799}} = 0,0015...\) và \(\frac{{0,1}}{{10,3}} = 0,0097...\)
\( \Rightarrow \frac{{21}}{{13799}} < \frac{{0,1}}{{10,3}}\) hay phép đo ước lượng độ tuổi của vũ trụ có độ chính xác cao hơn.

Phương pháp 1: 67,31 \( \pm \)0,96
\(a = 67,31;d = 0,96\)
Sai số tương đối \({\delta _1} \le \frac{d}{{\left| a \right|}} = \frac{{0,96}}{{67,31}} \approx 0,014\)
Phương pháp 2: 67,90 \( \pm \)0,55
\(a = 67,90;d = 0,55\)
Sai số tương đối \({\delta _2} \le \frac{d}{{\left| a \right|}} = \frac{{0,55}}{{67,90}} \approx 8,{1.10^{ - 3}} = 0,0081\)
Phương pháp 3: 67,74 \( \pm \)0,46
\(a = 67,74;d = 0,46\)
Sai số tương đối \({\delta _3} \le \frac{d}{{\left| a \right|}} = \frac{{0,46}}{{67,74}} \approx 6,{8.10^{ - 3}} = 0,0068\)
Ta thấy \(0,014 > 0,0081 > 0,0068\)
=> phương pháp 3 chính xác nhất.

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)

Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).

a) * Lớp 10C:

* Lớp 10D:

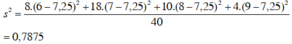
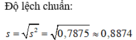
b) Kết quả lớp 10D có độ lệch chuẩn nhỏ hơn kết quả lớp 10C nên kết quả lớp 10D đồng đều hơn.



Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
Ta có bảng sau:
Giá trị
Độ lệch
Bình phương độ lệch
0,398
0,006
\(3,{6.10^{ - 5}}\)
0,399
0,005
\(2,{5.10^{ - 5}}\)
0,408
0,004
\(1,{6.10^{ - 5}}\)
0,410
0,006
\(3,{6.10^{ - 5}}\)
0,406
0,002
\(0,{4.10^{ - 5}}\)
0,405
0,001
\(0,{1.10^{ - 5}}\)
0,402
0,002
\(0,{4.10^{ - 5}}\)
Tổng
\(12,{2.10^{ - 5}}\)
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.