Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=y\left(x^2-y^2\right)\left(x^2+y^2\right)-y\left(x^4-y^4\right)=y\left(x^4-y^4\right)-y\left(x^4-y^4\right)=0\)
b) \(B=\left(x-1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3\left(1-x\right)x=x^3-3x^2+3x-1-x^3-x^2-x+x^2+x+1-3x+3x^2=0\)
a: Ta có: \(A=y\left(x^2-y^2\right)\left(x^2+y^2\right)-y\left(x^4-y^4\right)\)
\(=y\left(x^4-y^4\right)-y\left(x^4-y^4\right)\)
=0
b: Ta có: \(B=\left(x-1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3x\left(1-x\right)\)
\(=x^3-3x^2+3x-1-x^3+1-3x+3x^2\)
=0

a) \(2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]-3\left[\left(x+y\right)^2-2xy\right]\)
\(=2\left(1-3xy\right)-3\left(1-2xy\right)\)
\(=2-6xy-3+6xy=-1\)
\(\Rightarrow\) Giá trị của biểu thức không phụ thuộc vào biến \(x,y\)
b) \(\dfrac{\left(x+5\right)^2+\left(x-5\right)^2}{x^2+25}\)
\(=\dfrac{x^2+10x+25+x^2-10x+25}{x^2+25}\)
\(=\dfrac{2x^2+50}{x^2+25}=\dfrac{2\left(x^2+25\right)}{x^2+25}=2\)
\(\Rightarrow\) Giá trị của biểu thức không phụ thuộc vào biến \(x\)

1.
\(a,\left(-xy\right)\left(-2x^2y+3xy-7x\right)\)
\(=2x^3y^2-3x^2y^2+7x^2y\)
\(b,\left(\dfrac{1}{6}x^2y^2\right)\left(-0,3x^2y-0,4xy+1\right)\)
\(=-\dfrac{1}{20}x^4y^3-\dfrac{1}{15}x^3y^3+\dfrac{1}{6}x^2y^2\)
\(c,\left(x+y\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x+y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(d,\left(x-y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3\)
\(=x^3-3x^2y+3xy^2-y^3\)
2.
\(a,\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
\(b,\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
\(c,\left(4x-1\right)\left(6y+1\right)-3x\left(8y+\dfrac{4}{3}\right)\)
\(=24xy+4x-6y-1-24xy-4x\)
\(=\left(24xy-24xy\right)+\left(4x-4x\right)-6y-1\)
\(=-6y-1\)
#Toru

a: Ta có: \(y\left(x^2-y^2\right)\cdot\left(x^2+y^2\right)-y\left(x^4-y^4\right)\)
\(=y\left(x^4-y^4\right)-y\left(x^4-y^4\right)\)
=0
b: Ta có: \(\left(2x+\dfrac{1}{3}\right)\left(4x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)-\left(8x^3-\dfrac{1}{27}\right)\)
\(=8x^3+\dfrac{1}{27}-8x^3+\dfrac{1}{27}\)
\(=\dfrac{2}{27}\)
c: Ta có: \(\left(x-1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3x\left(1-x\right)\)
\(=x^3-3x^2+3x-1-x^3+1-3x+3x^2\)
=0

Bài \(3\)
\(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-\left(2x^2-6x\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
\(=\left(2x^2-2x^2\right)+\left(3x-10x+6x+x\right)+\left(-15+7\right)\)
\(=-8\)
Vậy biểu thức không phụ thuộc vào biến
\(B=4\left(y-6\right)-y^2\left(2+3y\right)+y\left(5y-4\right)+3y^2\)
Đề như này à?
Bài \(4\)
\(a,4a^2-16b^2=4\left(a^2-4b^2\right)=4\left(a-2b\right)\left(a+2b\right)\)
\(b,4x^2-4x+1=\left(2x\right)^2-2.2x.1+1^2=\left(2x+1\right)^2\)
\(c,\) ?
\(d,\left(x-y\right)^2-\left(2x-y\right)^2\\ =\left[\left(x-y\right)-\left(2x-y\right)\right]\left[\left(x-y\right)+\left(2x-y\right)\right]\\ =\left(x-y-2x+y\right)\left(x-y+2x-y\right)\\ =\left(-x\right)\left(3x-2y\right)\)
\(e,8x^3-y^3=\left(2x\right)^3-y^3\\ =\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(i,3x+6y+\left(x+2y\right)\\ =3\left(x+2y\right)+\left(x+2y\right)\\ =4\left(x+2y\right)\)
\(j,ax-ay-x+y=\left(ãx-ay\right)-\left(x-y\right)\\ =a\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(a-1\right)\)
`k,` `y` hay `y^2` ạ? vì nó mới phân tích được nhân tử.

`B = x^2- 2xy + y^2 + 2x - 10y + 17
`2B = 2x^2 - 4xy + 2y^2 + 4x - 20y + 34`
`= (x-y)^2 + (x+2)^2 + (y-5)^2 + 5 >= 5`.

\(a,VP=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ =\left(x+2y\right)\left[x^2-x.2y+\left(2y\right)^2\right]\\ =x^3+\left(2y\right)^3=x^3+8y^3=VT\left(đpcm\right)\\ b,VT=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(x-y\right)\\ =x^3-y^3-3xy\left(x-y\right)\\ =x^3-3x^2y+3xy^2-y^3\\ =\left(x-y\right)^3=VP\left(đpcm\right)\)
\(c,VT=\left(x-3y\right)\left(x^2+3xy+9y^2\right)-\left(3y+x\right)\left(9y^2-3xy+x^2\right)\\ =\left(x-3y\right)\left[x^2+x.3y+\left(3y\right)^2\right]-\left(x+3y\right).\left[x^2-x.3y+\left(3y\right)^2\right]\\ =x^3-27y^3-\left(x^3+27y^3\right)\\ =-54y^3=VP\left(đpcm\right)\)

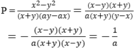
chỉ cần nhân ra là ok
đơn giãn mà
giải hộ mink vs, mink k hỉu lm