Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong mp (ACD) kéo dài MN và CD cắt nhau tại I
Trong mp (BCD) nối IQ cắt BD tại J
Áp dụng định lý Menelaus trong tam giác ACD:
\(\dfrac{AM}{MC}.\dfrac{CI}{ID}.\dfrac{DN}{NA}=1\Rightarrow1.\dfrac{CI}{ID}.\dfrac{1}{2}=1\Rightarrow IC=2ID\)
Do \(BC=4BQ\Rightarrow QC+QB=4QB\Rightarrow QC=3QB\)
Menelaus cho tam giác BCD:
\(\dfrac{QC}{QB}.\dfrac{BJ}{JD}.\dfrac{DI}{IC}=1\Rightarrow3.\dfrac{BJ}{JD}.\dfrac{1}{2}=1\Rightarrow\dfrac{BJ}{JD}=\dfrac{2}{3}\)
Menelaus cho tam giác CQI:
\(\dfrac{ID}{DC}.\dfrac{CB}{BQ}.\dfrac{QJ}{JI}=1\Rightarrow1.4.\dfrac{JQ}{JI}=1\Rightarrow\dfrac{JQ}{JI}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{JB}{JD}+\dfrac{JQ}{JI}=\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{11}{12}\)

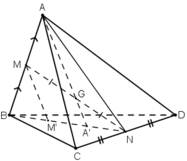
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
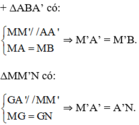
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.

Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)

Câu 1:
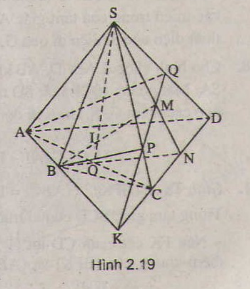
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
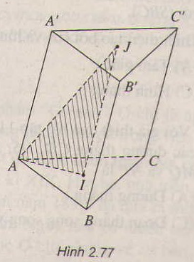
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy

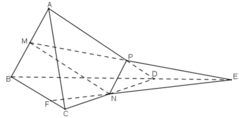
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

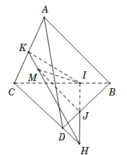
Trong mặt phẳng (BCD); IJ cắt CD tại H nên H thuộc (ACD)
Điểm H thuộc IJ m suy ra bốn điểm M; I; J; H đồng phẳng.
Nên trong mặt phẳng (IJM) , MH cắt IJ tại H và M H ⊂ I J M .
Mặt khác M ∈ A C D H ∈ A C D ⇒ M H ⊂ A C D .
Vậy giao tuyến của 2 mặt phẳng (ACD) và ( IJM) là MH
Chọn D.

Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
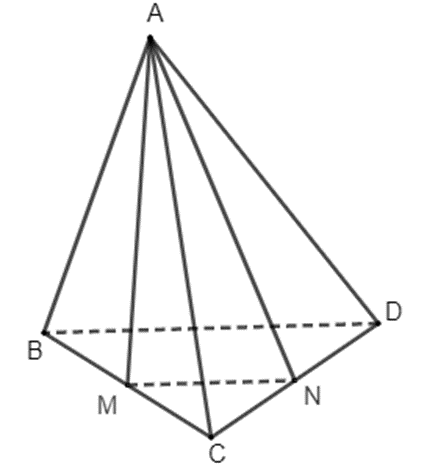
Vì M, N lần lượt là trung điểm của hai cạnh BC, CD nên MN là đường trung bình của tam giác BCD, suy ra MN // BD.
Mà đường thẳng MN nằm trong mặt phẳng (AMN).
Do đó, đường thẳng BD song song với mặt phẳng (AMN).

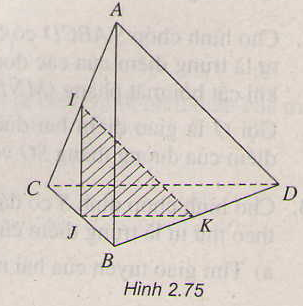
Trong mp(BCD), gọi E là giao điểm của JK và CD
Ta có: \(IE\cap AD=\left\{F\right\}\)
\(IE\subset\left(IJK\right)\)
Do đó: \(AD\cap\left(IJK\right)=F\)
Xét ΔACD có I,F,E thẳng hàng
nên \(\dfrac{AI}{IC}\cdot\dfrac{CE}{ED}\cdot\dfrac{DF}{FA}=1\)
=>\(1\cdot2\cdot\dfrac{DF}{FA}=1\)
=>\(\dfrac{FD}{FA}=\dfrac{1}{2}\)
=>\(\dfrac{FA}{FD}=2\)

Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ