Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Ta có: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên KE=KH
=>ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{ABC}\)(hai góc so le trong, HE//AB)
nên \(\widehat{KEH}=\widehat{ABC}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{HAD}=\widehat{HED}\)
Ta có: \(\widehat{DEK}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{ABC}+\widehat{HAB}\)
\(=90^0\)
=>DE\(\perp\)EK
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ΔHDB vuông tại D
mà DI là đường trung tuyến
nên \(DI=IH=IB\)
Xét ΔIHD có IH=ID
nên ΔIHD cân tại I
=>\(\widehat{IHD}=\widehat{IDH}\)
mà \(\widehat{IHD}=\widehat{HCA}\)(hai góc đồng vị, HD//AC)
nên \(\widehat{IDH}=\widehat{HCA}\)
ADHE là hình chữ nhật
=>\(\widehat{EAH}=\widehat{EDH}\)
=>\(\widehat{EDH}=\widehat{HAC}\)
\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)
\(=\widehat{HAC}+\widehat{HCA}\)
\(=90^0\)
=>DI\(\)\(\perp\)DE
c: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên EK=KH=KC
Xét ΔKEH có KE=KH
nên ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{CBA}\)(hai góc đồng vị, HE//AB)
nên \(\widehat{KEH}=\widehat{CBA}=\widehat{HBA}\)
ADHE là hình chữ nhật
=>\(\widehat{HAD}=\widehat{HED}\)
=>\(\widehat{HED}=\widehat{HAB}\)
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{HAB}+\widehat{HBA}=90^0\)
=>KE\(\perp\)DE
Ta có: KE\(\perp\)DE
ID\(\perp\)KE
Do đó: ID//KE
Xét tứ giác KEDI có
KE//DI
KE\(\perp\)ED
Do đó: KEDI là hình thang vuông
d: DI=1cm
mà HB=2DI
nên HB=2*1=2=2cm
EK=4cm
mà CH=2EK
nên \(CH=2\cdot4=8cm\)
BC=BH+CH
=2+8
=10cm
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot6\cdot10=30\left(cm^2\right)\)
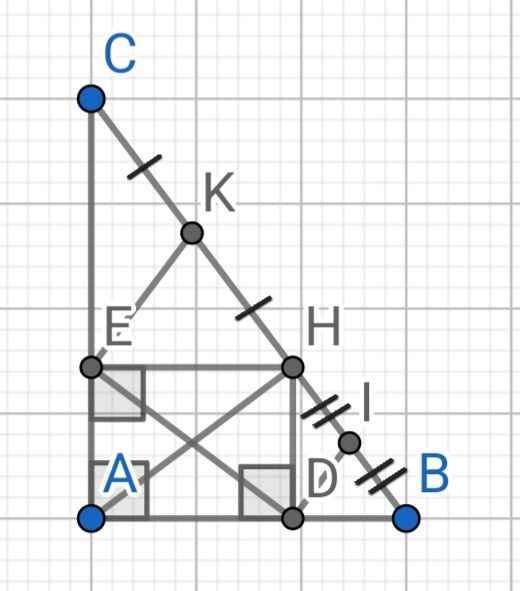a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE
a) Xét tứ giác ADHE có
\(\widehat{EAD}=90^0\)(\(\widehat{BAC}=90^0\), E∈AC, D∈AB)
\(\widehat{ADH}=90^0\)(HD⊥AB)
\(\widehat{AEH}=90^0\)(HE⊥AC)
Do đó: ADHE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Xét ΔCEH vuông tại E có EM là đường trung tuyến ứng với cạnh huyền CH(M là trung điểm của CH)
nên \(EM=\dfrac{CH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(MH=\dfrac{CH}{2}\)(M là trung điểm của CH)
nên EM=MH
Xét ΔMEH có ME=MH(cmt)
nên ΔMEH cân tại M(Định nghĩa tam giác cân)
⇒\(\widehat{MEH}=\widehat{MHE}\)(hai góc ở đáy)
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
a) Xét tứ giác EAFH có
\(\widehat{AFH}=90^0\)
\(\widehat{FAE}=90^0\)
\(\widehat{AEH}=90^0\)
Do đó: EAFH là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: \(\widehat{IAC}=90^0-\widehat{AFE}\)
\(\widehat{ICA}=90^0-\widehat{B}\)
mà \(\widehat{AFE}=\widehat{B}\left(=\widehat{HAC}\right)\)
nên \(\widehat{IAC}=\widehat{ICA}\)
mà \(\widehat{IBA}=90^0-\widehat{ICA}\)
và \(\widehat{IAB}=90^0-\widehat{IAC}\)
nên \(\widehat{IAB}=\widehat{IBA}\)
Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)
nên ΔIAB cân tại I(Định lí đảo của tam giác cân)
Xét ΔIAC có \(\widehat{IAC}=\widehat{ICA}\)(cmt)
nên ΔIAC cân tại I(Định lí đảo của tam giác cân)
Ta có: IA=IB(ΔIAB cân tại I)
IA=IC(ΔIAC cân tại I)
Do đó: IB=IC
mà I nằm giữa B và C
nên I là trung điểm của BC(Đpcm)
