Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật

Xl bạn trình độ mik chỉ làm đc vậy thôi nha!
Chứng minh
a, Xét tứ giác ANEF có:
Góc NAF= 900 ( vì ΔABC vuông tại A)
Góc ANF= 900 (vì EN⊥ AC)
Góc AFE= 900 ( vì EF ⊥ AB)
⇒ Tứ giác ANEF là hình chữ nhật( đpcm)
b)Xét tam giác BAC vuông tại A có:
AE là đường trung tuyến(BE=EC)
\(\Rightarrow\)AE=BE=EC
Xét t/g AEBD có:
BF=FA(EF vuông góc BA)
DF=FE(D đx với E qua F)
\(\Rightarrow\)T/g AEBD là hbh
Mà AE=BE(cmt)
\(\Rightarrow\)T/g AEBD là hthoi

Lời giải:
a. $M,E$ là trung điểm $BC, AC$
$\Rightarrow ME$ là đường trung bình của $ABC$ ứng với $AB$
$\Rightarrow ME\parallel AB$
Mà $AB\perp AC$ nên $ME\perp AC$
$\Rightarrow \widehat{E}=90^0$
Tứ giác $ADME$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên là hcn.
b.
Tứ giác $AMKC$ có 2 đường chéo $AC, MK$ cắt nhau tại trung điểm $E$ của mỗi đường nên là hình bình hành.
Mà $MK\perp AC$ (do $ME\perp AC$)
$\Rightarrow AMKC$ là hình thoi.
c.
Gọi I là giao $DE, HM$
$DM\perp AB, AB\perp AC\Rightarrow DM\parallel AC$
$\Rightarrow \frac{DB}{AD}=\frac{BM}{MC}=1$ (định lý Talet)
$\Rightarrow DB=AD$ hay $D$ là trung điểm $AB$
$ME$ là đường trung bình ứng với cạnh AB
$\Rightarrow ME\parallel AB$ và $ME=\frac{1}{2}AB$
Mà $E$ là trung điểm của $MK$
$\Rightarrow EK\parallel AB$ và $EK=AB:2$
$\Rightarrow EK\parallel DA$ và $EK=DA$
$\Rightarrow DEKA$ là hbh
$\Rightarrow DE\parallel AK$
Mà $HM\perp AK$ nên $DE\perp HM(*)$
Lại có:
$DE\parallel AK \Rightarrow IE\parallel HK$
$\Rightarrow \frac{MI}{IH}=\frac{ME}{EK}=1$
$\Rightarrow MI=IH(**)$
Từ $(*); (**)$ suy ra $DE\perp HM$ tại trung điểm $I$ của $HM$
$\Rightarrow DE$ là đường trung trực của $HM$
$\Rightarrow DH=DM, EH=EM$
$\Rightarrow \triangle DHE=\triangle DME$ (c.c.c)
$\Rightarrow \widehat{DHE}=\widehat{DME}=90^0$
$\Rightarrow DH\perp HE$

a: Xét tứ giác AKMN có
MN//AK
AN//MK
Do đó: AKMN là hình bình hành
mà \(\widehat{NAK}=90^0\)
nên AKMN là hình chữ nhật
b: Xét ΔAMQ có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAMQ cân tại A
mà AN là đường cao
nên AN là tia phân giác của góc MAQ(1)
Xét ΔAME có
AK là đường cao
AK là đường trung tuyến
DO đó: ΔAME cân tại A
mà AK là đường cao
nên AK là tia phân giác của góc MAE(2)
Từ (1) và (2) suy ra \(\widehat{QAE}=2\cdot\left(\widehat{MAN}+\widehat{MAK}\right)=2\cdot90^0=180^0\)
hay Q,E,A thẳng hàng

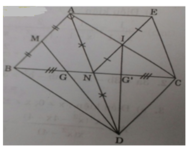
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành

Chưa có ai trả lời câu hỏi này, hãy gửi một câu trả lời để giúp tran cong hoai giải bài toán này.
a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: Đề sai rồi bạn
AM//NB mà

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
Suy ra: AM=EF
hay EF=5cm

a: Xét tứ giác AMHK có
góc AMH=góc AKH=góc KAM=90 độ
=>AMHK là hình chữ nhật
=>AH=MK
b: Xét ΔAHD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAHD cân tại A
=>AH=AD và AB là phân giác của góc HAD(1)
Xét ΔHEA có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAHE cân tại A
=>AH=AE và AC là phân giác của góc HAE(2)
Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔAHB và ΔADB có
AH=AD
góc HAB=góc DAB
AB chung
=>ΔAHB=ΔADB
=>góc ADB=90 dộ
=>BD vuông góc DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
góc HAC=góc EAC
AC chung
=>ΔAHC=ΔAEC
=>goc AEC=90 độ
=>CE vuông góc ED(4)
Từ (3), (4) suy ra BD//CE
chịu@@@@@@@@@@@@@@@@@@
cũng biết làm nhưng ko