Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TK
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

Để chứng minh các phần a, b và c, ta sẽ sử dụng các tính chất của tam giác vuông và hình chữ nhật.
a. Ta có tam giác ABC vuông tại A, nên theo định lí trung tuyến, ta có DE là đường trung tuyến của tam giác ABC. Do đó, DE song song với cạnh AC. Tương tự, ta có DF song song với cạnh AB. Vậy DE//AC và DF//AB.
b. Ta cần chứng minh AEDF là hình chữ nhật. Đầu tiên, ta thấy DE//AC và DF//AB (theo phần a). Khi đó, ta có:
- AD = DC (vì D là trung điểm của BC)
- AE = EB (vì E là trung điểm của AB)
- AF = FC (vì F là trung điểm của AC)
Vậy ta có các cạnh đối diện của tứ giác AEDF bằng nhau, do đó AEDF là hình chữ nhật.
c. Gọi M là điểm đối xứng của D qua AB. Ta cần chứng minh M đối xứng với N qua A. Để làm điều này, ta sẽ chứng minh AM = AN và góc MAN = góc NAM.
- Vì M là điểm đối xứng của D qua AB, nên ta có AM = AD.
- Vì N là điểm đối xứng của D qua AC, nên ta có AN = AD.
Do đó, ta có AM = AN.
- Ta có góc MAD = góc DAB (vì M là điểm đối xứng của D qua AB)
- Ta có góc NAD = góc DAC (vì N là điểm đối xứng của D qua AC)
Vì tam giác ABC vuông tại A, nên góc DAB = góc DAC. Từ đó, ta có góc MAD = góc NAD.
Vậy ta có AM = AN và góc MAN = góc NAM, do đó M đối xứng với N qua A.
Vậy ta đã chứng minh được M đối xứng với N qua A.

TK
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
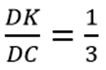
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
SDGB là S tam giác DGB pk ạ ?