Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta thấy:
$S_{ABN}+S_{BCN}=S_{ABC}=210$ (cm2)
$\frac{S_{ABN}}{S_{BCN}}=\frac{AN}{CN}=\frac{2}{3}$
Tổng số phần bằng nhau: $2+3=5$ (phần)
Diện tích $ABN$ là: $210:5\times 2=84$ (cm2)
Diện tích $BCN$: $210-84=126$ (cm2)

Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90

Gợi ý:
A) Diện tích tam giác ABC
- Gọi S là diện tích tam giác ABC, h là độ cao của tam giác ABC kẻ từ đỉnh B xuống AC.
- Theo định lý diện tích tam giác, ta có: S = (1/2)AC.h
- Theo giả thiết, ta có: AN = (2/3)NC, suy ra AC = AN + NC = (2/3)NC + NC = (5/3)NC
- Do đó, S = (1/2).(5/3)NC.h = (5/6)NC.h
- Gọi S1 là diện tích tam giác ABM, h1 là độ cao của tam giác ABM kẻ từ đỉnh B xuống AM.
- Theo định lý diện tích tam giác, ta có: S1 = (1/2)AM.h1
- Theo giả thiết, ta có: S1 = 30cm2
- Do M là điểm nằm trên AC, nên AM = AN + NM = (2/3)NC + NM
- Do đó, S1 = (1/2).[(2/3)NC + NM].h1 = 30cm2
- Ta có hai phương trình với hai ẩn số NC và h1, ta có thể giải hệ phương trình này để tìm được NC và h1.
- Sau khi tìm được NC và h1, ta có thể thay vào công thức S = (5/6)NC.h để tính được diện tích tam giác ABC.
B) Diện tích tam giác ABN
- Gọi S2 là diện tích tam giác ABN, h2 là độ cao của tam giác ABN kẻ từ đỉnh B xuống AN.
- Theo định lý diện tích tam giác, ta có: S2 = (1/2)AN.h2
- Theo giả thiết, ta có: AN = (2/3)NC
- Do đó, S2 = (1/2).(2/3)NC.h2 = (1/3)NC.h2
- Ta có thể sử dụng quan hệ giữa các độ cao của tam giác ABC, ABM và ABN để tìm được h2 theo h1.
- Sau khi tìm được h2, ta có thể thay vào công thức S2 = (1/3)NC.h2 để tính được diện tích tam giác ABN.

theo đề bài ta có thể chia hình tam giác này thành 3 phần và hình tam giác ABN bằng 1 phần hình BNC bằng 2 phần nên :
a SABN=1/2 SBNC
b SBNC=2/3 SABC

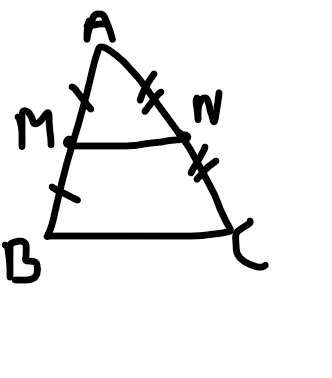
a,có:S AMN =1/2 S ABC
=>S ABC = 2.5 AMN = 2.3=6 cm2
b,có 2.MN=BC
=>MN=BC/2 = 6/2 = 3 cm

Muốn tính diện tích hình tam giác độ dài đáy nhân với chiều cao rồi nhân cho 2 nhé bạn
muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2
Kẻ BK vuông góc với AC
\(S_{ABN}=\dfrac{1}{2}\cdot BK\cdot AN\)
\(S_{ACB}=\dfrac{1}{2}\cdot BK\cdot AC\)
=>\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{AN}{AC}=\dfrac{2}{5}\)
=>\(S_{ABN}=72\left(cm^2\right)\)
=>\(S_{BCN}=108\left(cm^2\right)\)