Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔBHA vuông tại H
=>BH<AB
ΔCKA vuông tại K
=>CK<AC
=>BH+CK<AB+AC
b: ΔBDH vuông tại H
=>BH<BD
ΔCKD vuông tại K
=>CK<CD
=>BH+CK<BD+CD=BC

a. xét tam giác vuông AHB và tam giác vuông AHC
\(AB>AH\) ( BĐT tam giác )
\(AC>AH\) ( BĐT tam giác )
\(\Rightarrow AB+AC>2.AH\) hay \(AH< \dfrac{AB+AC}{2}\)
b.xét tam giác ABM và tam giác ACM, có:
AB = AC ( ABC cân )
góc BAM = góc CAM ( ABC cân )
AM : cạnh chung
Vậy tam giác ABM = tam giác ACM ( c.g.c )
=> MB = MC ( 2 cạnh tương ứng )
a. -Vì AH⊥BC tại H (gt).
Nên AH là đường vuông góc, AB, AC là các đường xiên.
\(\Rightarrow AH< AB;AH< AC\) (quan hệ giữa đường vuông góc và đường xiên).
\(\Rightarrow AH+AH< AB+AC\)
\(\Rightarrow2AH< AB+AC\)
\(\Rightarrow AH< \dfrac{AB+AC}{2}\)
b. -Có: AH⊥BC tại H (gt).
Nên BH, CH lần lượt là hình chiếu của đường xiên AB,AC lên BC.
Mà \(AB< AC\) (gt)
\(\Rightarrow BH< CH\) (quan hệ giữa đường xiên và hình chiếu).
-Có: MH⊥BC tại H (gt).
Nên BH, CH lần lượt là hình chiếu của đường xiên MB,MC lên BC.
Mà \(BH< CH\left(cmt\right)\)
\(\Rightarrow MB< MC\)(quan hệ giữa đường xiên và hình chiếu).

a: Xét ΔABC có AC>AB
mà HC,HB lần lượt là hình chiếu của AC,AB trên BC
nên HC>HB
b: Xét ΔDBC có HB<HC
mà HB,HC lần lượt là hình chiếu của DB,DC trên BC
nên DB<DC

ΔAED vuông tại E
=>AD là cạnh lớn nhất trong ΔAED
=>AD>AE
Ta có: ΔCFD vuông tại F
=>CD là cạnh lớn nhất trong ΔCFD
=>CD>CF
Ta có: AD>AE
CD>CF
Do đó: AD+CD>AE+CF
=>AC>AE+FC

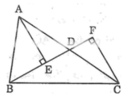
+ AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BF
⇒ AE < AD. ( quan hệ đường vuông góc và đường xiên). (1)
+ CF là đường vuông góc hạ từ đỉnh C xuống đường thẳng BF
⇒ CF < CD ( quan hệ đường vuông góc và đường xiên). (2)
Từ (1) và (2) vế cộng vế ta được: AE + CF < AD + CD = AC.

Ta có : AC<AB
=>HC<HB
Mà : HC<HB
Nên : EC<EB
Vậy : đpcm