Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*OLM đang lỗi nên không vẽ được hình, bạn vào thống kê mình để xem hình nhé! Mình vẽ ở GeoGebra*

a \(\hept{\begin{cases}S_{BHC}=\frac{1}{2}\cdot BC\cdot HD\\S_{ABC}=\frac{1}{2}\cdot BC\cdot AD\end{cases}}\Rightarrow\frac{HD}{AD}=\frac{S_{BHC}}{S_{ABC}}\)
Tương tự cũng có: \(\hept{\begin{cases}\frac{HE}{BE}=\frac{S_{AHC}}{S_{ABC}}\\\frac{HF}{CF}=\frac{S_{AHB}}{S_{ABC}}\end{cases}}\)
\(\Rightarrow\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
b) Xét \(\Delta BHD\) và \(\Delta BCE\)có:
\(\widehat{B}\)chung
\(\widehat{BDH}=\widehat{BEC}=90^o\)
=> \(\Delta BHD\)đồng dạng với \(\Delta\)BEC (g.g)
=> \(\frac{BH}{BC}=\frac{BD}{BE}\Rightarrow BH\cdot BE=BC\cdot BD\left(1\right)\)
Cmtt: \(\Delta CHD\)đồng dạng \(\Delta CBF\)(g.g)
=> \(\frac{CH}{CB}=\frac{CD}{CF}\Rightarrow CH\cdot CF=CB\cdot CD\left(2\right)\)
Từ (1) (2) => \(CH\cdot CF+BH\cdot BE=BC\cdot BD+CD\cdot CB=BC^2\)
c) \(\widehat{HDC}=\widehat{HEC}=90^o\)
=> Tứ giác HDCE nội tiếp
=> \(\widehat{HED}=\widehat{HCD}\)(3)
\(\widehat{AFH\:}=\widehat{AEH}=90^o\)
=> AFHE nội tiếp
=> \(\widehat{FEH}=\widehat{FAH}\left(4\right)\)
Mà \(\widehat{FAH}=\widehat{HCD}\) (cùng phụ \(\widehat{ABC}\)) (5)
(3)(4)(5)=> \(\widehat{FEH}=\widehat{HED}\)
=> EH là phân giác \(\widehat{FED}\)
Cmtt cũng được: DH là phân giác \(\widehat{FDE}\)và FH là phân giác \(\widehat{DFE}\)
=> H là tâm đường tròn nội tiếp tam giác EFD
=> H cách đều EF; FD; ED
d) Gọi O là giao của phân giác \(\widehat{BHC}\)và trung trực của CH. Theo gt thì điểm O cố đnhj
Ta có: OH=OC => \(\Delta\)HOC cân tại O => \(\widehat{CHO}=\widehat{HCO}\)
Mà \(\widehat{BHO}=\widehat{CHO}\)nên \(\widehat{MHO}=\widehat{NCO}\)
=> \(\Delta OMH=\Delta ONC\left(cgc\right)\)
=> OM=ON
=> O thuộc đường trung trực của MN, hay đường trung trực của MN luôn đi qua 1 điểm cố định
@qu y nh Bạn có thể làm ý c theo cách khác giúp mk đc không ạ!!! Mk chưa học tứ giác nội tiếp(Nội dung lớp 9)
 Nguồn: Lazi.
Nguồn: Lazi.
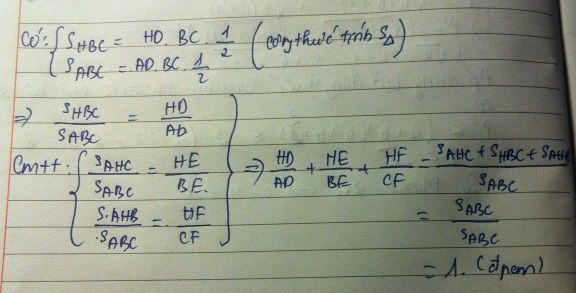
a,Ta có \(\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{1}{2}HD.BC}{\frac{1}{2}AD.BC}=\frac{HD}{AD}\)
tương tự \(\frac{S_{HAC}}{S_{ABC}}=\frac{HE}{BE};\frac{S_{HAB}}{S_{ABC}}=\frac{HF}{CF}\)
\(\Rightarrow\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{HBC}}{S_{ABC}}+\frac{S_{HAC}}{S_{ABC}}+\frac{S_{HAB}}{S_{ABC}}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\left(ĐPCM\right)\)
b, bổ sung đề rồi mình làm tiếp cho ạ
Câu b) em có cách này cô ạ, cô check giùm em xem có đúng không ạ :
Ta có : \(\frac{HA}{AD}=\frac{S_{ABH}}{S_{ABD}}=\frac{S_{AHC}}{S_{ADC}}=\frac{S_{ABH}+S_{AHC}}{S_{ABD}+S_{ADC}}=\frac{S_{ABH}+S_{AHC}}{S_{ABC}}\)
( Tính chất dãy tỉ số bằng nhau )
Tương tự ta có :
\(\frac{HB}{BE}=\frac{S_{AHB}+S_{BHC}}{S_{ABC}}\), \(\frac{HC}{CF}=\frac{S_{AHC}+S_{BHC}}{S_{ABC}}\)
Khi đó : \(\frac{HA}{AD}+\frac{HB}{BE}+\frac{HC}{CF}=\frac{2\left(S_{ABH}+S_{AHC}+S_{BHC}\right)}{S_{ABC}}=\frac{2S_{ABC}}{S_{ABC}}=2\)
Vậy : \(\frac{HA}{AD}+\frac{HB}{BE}+\frac{HC}{CF}=2\)