Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác AHB vuông tại H => Áp dụng định lý pitago ta có :
AB2 = AH2 + HB2 => HB2 = AB2 - AH2 = 252 - 242 = 625 - 576 = 49 = 72
=> HB = 7
Tam giác AHC vuông tại H => Áp dụng định lý pitago ta có :
AC2 = CH2 + AH2 => CH2 = AC2 - AH2 = 262 - 242 = 676 - 576 = 100 = 102
=> CH = 10
=> BC = HB + CH = 7 + 10 = 17 (cm)
Vậy BC = 17 (cm)
Giải:
Áp dụng định lý Py-ta-go vào tam giác AHB (tam giác AHB vuông tại H)
=> AB2 = AH2 + HB2
=> HB2 = AB2 - AH2
=> HB2 = 252 - 242
=> HB = 625 - 526 = 49 = 72
=> HB = 7
Áp dụng định lý Py-ta-go và tam giác AHC (tam giác AHC vuông H)
=> AC2 = AH2 + HC2
=> HC2 = AC2 - AH2
=> HC2 = 262 - 242
=> HC = 676 - 576 = 100 = 102
=> HC = 10
=> BC = BH + HC
BC = 7 + 10 = 17 (cm)
Vậy BC = 17 cm.

a) Xét hai tam giác AHB và AHC ta có
AB = AC (gt)
\(\widehat{B}=\widehat{C}\)(gt)
BH = HC (gt)
Do đó: \(\Delta AHB=\Delta AHC\)(c-g-c)
b) Ta có: \(\Delta AHB=\Delta AHC\)(câu a)
=> \(\widehat{AHB}=\widehat{AHC}\)(cặp góc tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)(kề bù)
=> \(\widehat{AHB}=\widehat{AHC}=90^o\)
c) Ta có BH = HC (gt)
Mà BH + HC = BC
hay BH + HC = 10 (cm)
=> BH = HC = 5 (cm)
Áp dụng định lí Py-ta-go vào tam giác vuông ABH có
\(AB^2-BH^2=AH^2\)
\(13^2-5^2=AH^2\)
\(12^2=AH^2\)
=> AH = 12
P/s: k hộ thần =))))

Áp dụng định lí Pi-ta-go \(\Delta\) vuông ABH ta có:
AH2 + BH2 = AB2
=> BH2 = AB2 - AH2
hay BH2 = 25 - 24 = 1 cm
=> BH = 0,5 cm
Áp dụng định lí Pi-ta-go vào \(\Delta\) vuông AHC ta có:
AH2 + HC2 = AC2
=> HC2 = AC2 - AH2
hay HC2 = 26 - 24 = 2
=> HC = 1 cm
Vì BC = HC + BH
=> BC = 1 + 0,5 = 1,5 cm
=> BC = 1,5 cm (số nhỏ v chưởng)
\(\Delta ABH\) vuông tại H, theo định lí Py-ta-go ta có:
AB2 = AH2 + BH2
\(\Rightarrow\) BH2 = AB2 - AH2
BH2 = 252 - 242
BH2 = 49
\(\Rightarrow\) BH = \(\sqrt{49}\) = 7 (cm)
\(\Delta ACH\) vuông tại H, theo định lí Py-ta-go ta có:
AC2 = AH2 + CH2
CH2 = AC2 - AH2
CH2 = 262 - 242
CH2 = 100
\(\Rightarrow\) CH = \(\sqrt{100}\) = 10 (cm)
Mà BC = BH + CH
\(\Rightarrow\) BC = 7 + 10 = 17 (cm)
Vậy BC = 17 (cm).

Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
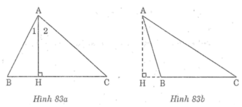
* Trường hợp Bnhọn (hình 83a)
Trong Δ ABC, ta có: AB < AC
Suy ra: ∠B > ∠C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC)
* Trường hợp Btù (hình 83b)
Vì điểm B nằm giữa H và C nên ∠(HAC) = ∠(HAB) + ∠(BAC)
Vậy ∠(HAB) < ∠(HAC).
TH1:B là góc nhọn:
Áp dụng định lý pitago cho tam giác ABH:
AH^2+BH^2=AB^2
<=>24^2+BH^2=25^2
<=>BH^2=49
<=>BH=7
Áp dụng định lý pitago cho tam giác AHC:
AH^2+HC^2=AC^2
<=>24^2+HC^2=26^2
<=>HC^2=100
<=>HC=10
Ta có:
BC=BH+HC=7+10=17(cm)
TH2:B là góc tù:
Áp dụng định lý pitago cho tam giác ABH:
AH^2+HB^2=AB62
<=>24^2+HB^2=25^2
<=>HB^2=49
<=>HB=7(cm)
Áp dụng định lý pitago cho tam giác AHC:
AH^2+HC^2=AC^2
<=>24^2+HC^2=26^2
<=>HC=10(cm)
Ta có:
BC=HC-HB=10-7=3(cm)
Mình sẽ giải trường hợp 1 trước nhé!
Ta có tam giác AHB vuông tại H
=> AB^2=AH^2+BH^2 (PYTAGO)
=> BH^2=AB^2-AH^2=25^2-24^2=49
=> BH=\(\sqrt{49}=7cm\)
Ta lại có tam giác AHC vuông tại H
=> AC^2=AH^2+HC^2 (PYTAGO)
=> HC^2=AC^2-AH^2=26^2-24^2=100
=> HC=\(\sqrt{100}\)=10 cm
Mà BH+HC=BC
=> BC=7+10=17 cm
Bạn mk nak!