Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

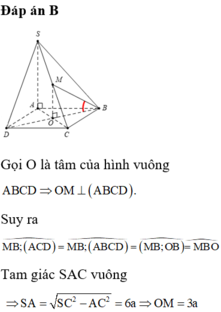
Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)

(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ

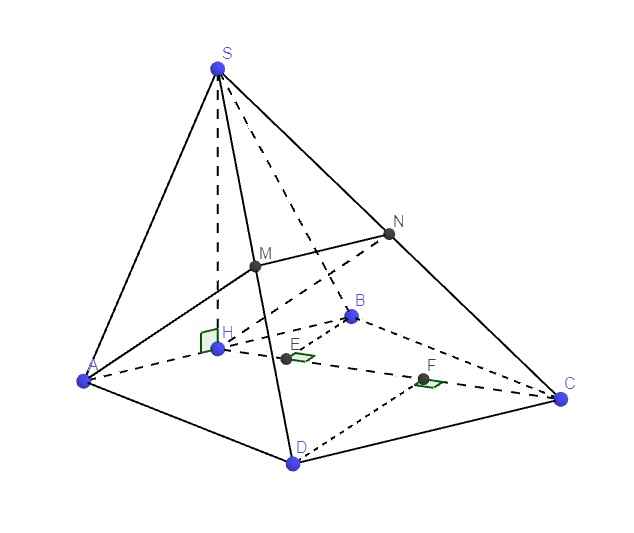
Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)

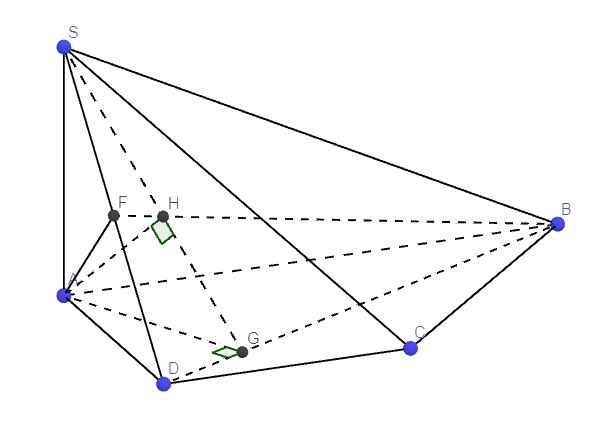
Kẻ \(AF\perp SD\) ; \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AF\)
\(\Rightarrow AF\perp\left(SCD\right)\)
Kẻ \(AG\perp BD\) ; trong mp (SBD) kẻ \(AH\perp SG\)
\(\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow\widehat{FAH}\) là góc giữa (SCD) và (SBD)
\(AH\perp\left(SBD\right)\Rightarrow AH\perp FH\Rightarrow\Delta FAH\) vuông tại H
Tam giác SAD vuông cân tại A \(\Rightarrow AF=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng tam giác SBD: \(\dfrac{1}{AG^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{5}{4a^2}\)
Hệ thức lượng tam giác SAG: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AG^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\Rightarrow AH=\dfrac{2a}{3}\)
\(\Rightarrow cos\widehat{FAH}=\dfrac{AH}{AF}=\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\widehat{FAH}\approx19^028'\)

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
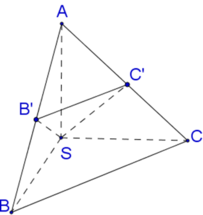
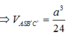




Đề đúng là SC vuông góc (ABCD) phải không nhỉ?
Gọi O là giao điểm AC và BD \(\Rightarrow\) O đồng thời là trung điểm AC và BD
Gọi E và F lần lượt là trung điểm SA và AD, từ O kẻ \(OH\perp EF\) (1)
OE là đường trung bình tam giác SAC \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}SC=\dfrac{3a}{2}\\OE||SC\Rightarrow OE\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow OE\perp AD\)
OF là đường trung bình tam giác ACD \(\Rightarrow\left\{{}\begin{matrix}OF||CD\Rightarrow OF\perp AD\\OF=\dfrac{1}{2}CD=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AD\perp\left(OEF\right)\) \(\Rightarrow AD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SAD\right)\)
\(\Rightarrow HD\) là hình chiếu vuông góc của OD lên (SAD)
\(\Rightarrow\widehat{HDO}\) là góc giữa BD và (SAD)
Hệ thức lượng: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}\Rightarrow OH=\dfrac{OE.OF}{\sqrt{OE^2+OF^2}}=\dfrac{3a\sqrt{10}}{20}\)
\(OD=\dfrac{1}{2}BD=\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow sin\widehat{HDO}=\dfrac{OH}{OD}=\dfrac{3\sqrt{2}}{10}\Rightarrow\widehat{HDO}\approx25^06'\)