Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Đường thẳng đi qua ĐCĐ, ĐCT là ∆ 1 : 2 x + y = 0 c ó V T P T n 1 ( 2 ; 1 )
Đường thẳng đã cho có ∆ : x + m y + 3 = 0 c ó V T P T n 2 ( 1 ; m )
Yêu cầu bài toán
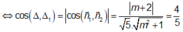
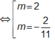
+ Đường thẳng đi qua 2 điểm cực trị của hàm số là 2x+ y=0 có VTPT n 1 → ( 2 ; 1 )
+ Đường thẳng đã cho x+ my+ 3= 0 có VTPT n 2 → ( 1 ; m )
Yêu cầu bài toán
Chọn A
Chọn C
Ta có y ' = 3 x 2 - 6 x + 3 m . Hàm số có hai điểm cực trị <=> y’=0 có hai nghiệm phân biệt
<=> Δ ' = 3 2 - 3 . 3 m > 0 <=> m < 1 (*)
Chia y cho y’ ta được:
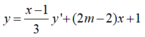
Giả sử x 1 , x 2 là hai nghiệm phân biệt của y’=0
Phương trình đường thẳng đi qua hai điểm cực trị có dạng (d) : y= (2m-2)x+1
(d) có vectơ pháp tuyến là n1→ = (2m - 2; -1)
(Δ) : 3x+y-8=0 có vectơ pháp tuyến là n2→(3; 1)
Vì góc giữa đường thẳng (d) và (Δ) là 45o nên
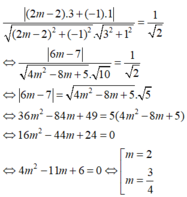
Đối chiếu điều kiện (*) có m = 3 4
Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.
Ta có 
Để đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó gọi A( 0 ; -3m-1) và B( 2m ; 4m3-3m-1) là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của AB là điểm I ( m ; 2m3-3m-1) và A B → = ( 2 m ; 4 m 3 ) = 2 m ( 1 ; 2 m 2 )
Đường thẳng d có một vectơ chỉ phương là u → = ( 8 ; - 1 ) .
Ycbt 
Chọn D.
Chọn C
.
Vì 
nên phương trình 
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị 
.
Giả sử hàm số có hai điểm cực trị lần lượt là 
và 
, với 
, 
là nghiệm của phương trình 
.
Thực hiện phép chia 
cho 
ta được : 
.
Khi đó ta có: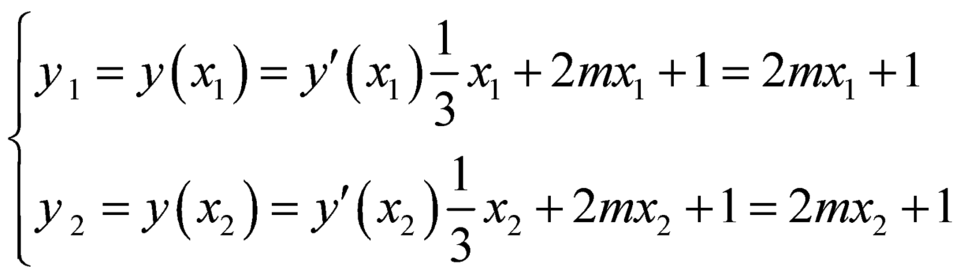 
.
Ta thấy, toạ độ hai điểm 
và 
thoả mãn phương trình 
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là 
.
Ta thấy 
luôn qua 
.
Đặt 
.
.
Xét hàm số 
, 
.
, 
.
Suy ra hàm số 
liên tục và đồng biến trên 
.
Do đó 
.
Vậy 
đạt giá trị lớn nhất 
.
Ta có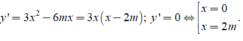 
Đề đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó tọa độ hai điểm cực trị là A( 0 ; 4m2- 2) và B( 2m; 4m2- 4m3-2).
Do I( 1; 0) là trung điểm của AB nên
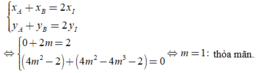
Chọn C.
Chọn A
Ta có 
và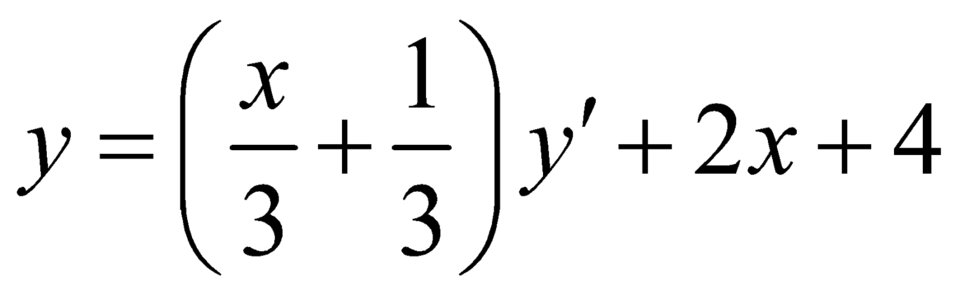 
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là 
, 
.
Đường tròn 
có tâm 
và bán kính 
.
Đường thẳng 
tiếp xúc với đường tròn 
khi và chỉ khi 
.
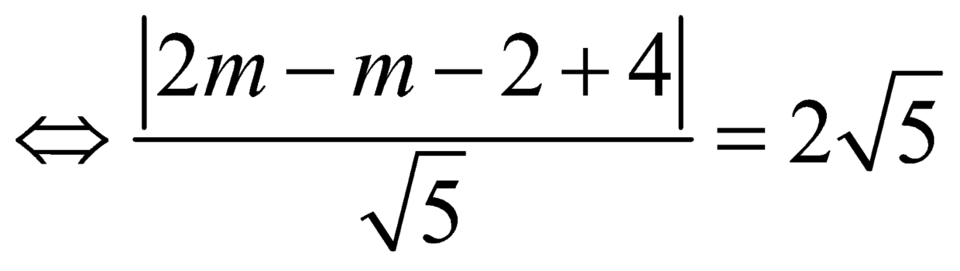
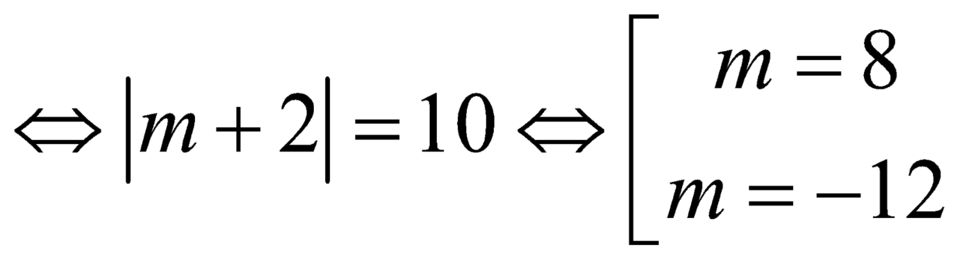Vậy 
.
Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 - 6 x - m
Hàm số có 2 cực trị m > -3 , gọi x 1 , x 2 là hai nghiệm của phương trình y ' = 0 ,
ta có: x 1 + x 2 = 2
Bấm máy tính
Hai điểm cực trị của đồ thị hàm số là
Gọi I là trung điểm của AB
⇒ I ( 1 ; - m )
Đường thẳng đi qua hai điểm cực trị là
Yêu cầu bài toán
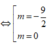
Kết hợp với điều kiện thì m = 0
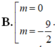
Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có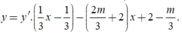
đường thẳng đi qua hai điểm cực trị Avà B là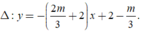
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng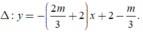
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
Suy ra
Chọn A.