Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 
Để đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó gọi A( 0 ; -3m-1) và B( 2m ; 4m3-3m-1) là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của AB là điểm I ( m ; 2m3-3m-1) và A B → = ( 2 m ; 4 m 3 ) = 2 m ( 1 ; 2 m 2 )
Đường thẳng d có một vectơ chỉ phương là u → = ( 8 ; - 1 ) .
Ycbt 
Chọn D.

Ta có
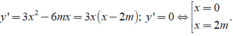
Hàm số có hai điểm cực trị khi y’= 0 có hai nghiệm phân biệt suy ra
0≠2m hay m≠0
Tọa độ các điểm cực trị của đồ thị hàm số là: A( 0; 2) và B( 2m; 2-4m3).
Suy ra ![]()
Theo giả thiết A; Bvà M thẳng hàng 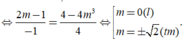
Chọn D.

Đáp án C
Ta có ![]()
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi ![]() Khi đó
Khi đó ![]() và B(2m;0).
và B(2m;0).
Vậy giá trị của m là ![]()

\(y'=3x^2-6mx=0\Rightarrow3x\left(x-2m\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2m\end{matrix}\right.\) (\(m\ne0\))
\(\Rightarrow\left[{}\begin{matrix}A\left(0;4m^2-2\right)\\B\left(2m;-4m^3+4m^2-2\right)\end{matrix}\right.\)
Bạn nên biết công thức này: công thức diện tích tam giác khi biết tọa độ 3 điểm:
\(S_{ABC}=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
Áp nó vào bài toán:
\(\left|2m.\left(6-4m^2\right)-1.\left(-4m^3+4m^2-2\right)\right|=8\)
\(\Leftrightarrow...\)

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.

Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có 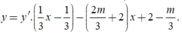
đường thẳng đi qua hai điểm cực trị Avà B là 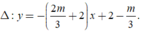
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng 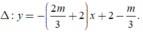 có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
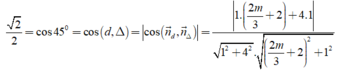
Suy ra
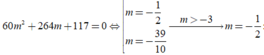 thỏa mãn
thỏa mãn
Chọn A.

+ Đạo hàm y’ = 3x2- 6mx= 3x( x- 2m)
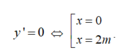
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi :m≠0. (1)
+ Tọa độ các điểm cực trị của đồ thị hàm số là A( 0 ; 3m3) ; B( 2m; -m3)
Ta có: O A → ( 0 ; 3 m 3 ) ⇒ O A = 3 m 3 ( 2 )
Ta thấy A ∈ O y ⇒ O A ≡ O y ⇒ d ( B ; O A ) = d ( B ; O y ) = 2 m (3)
+ Từ (2) và (3) suy ra S= ½. OA.d(B ; OA)=3m4.
Do đó: S ∆ O A B = 48 ⇔ 3 m 4 = 48 ⇔ m = ± 2 (thỏa mãn (1) ).
Chọn D.

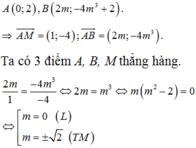
Ta có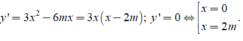
Đề đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó tọa độ hai điểm cực trị là A( 0 ; 4m2- 2) và B( 2m; 4m2- 4m3-2).
Do I( 1; 0) là trung điểm của AB nên
Chọn C.