Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho hai điểm A(1;2), B(4;3).tìm tọa độ điểm M biết MAB=135 độ, khoảng cách từ M đến AB bằng căn 10/2

Note: \(135^0=90^0+45^0\)
\(\overrightarrow{AB}=\left(3;1\right)\) \(\Rightarrow AB=\sqrt{10}\)
Phương trình AB:
\(1\left(x-1\right)-3\left(y-2\right)=0\Leftrightarrow x-3y-5=0\)
Phương trình đường thẳng d qua M và vuông góc d có dạng:
\(3x+y+c=0\)
Gọi N là giao điểm AB và d \(\Rightarrow\widehat{MAN}=180^0-135^0=45^0\)
\(\Rightarrow\Delta MAN\) vuông cân tại N \(\Rightarrow MN=AN=\frac{\sqrt{10}}{2}=\frac{AB}{2}\)
\(\Rightarrow\overrightarrow{NA}=\frac{1}{2}\overrightarrow{AB}\Rightarrow N\left(-\frac{1}{2};\frac{3}{2}\right)\)
\(N\in d\Rightarrow3\left(-\frac{1}{2}\right)+\frac{3}{2}+c=0\Rightarrow c=0\Rightarrow\) pt d: \(3x+y=0\)
\(\Rightarrow M\left(m;-3m\right)\Rightarrow\overrightarrow{NM}=\left(m+\frac{1}{2};-3m-\frac{3}{2}\right)\)
\(MN^2=\left(m+\frac{1}{2}\right)^2+\left(-3m-\frac{3}{2}\right)^2=\frac{5}{2}\Rightarrow m=...\)

Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
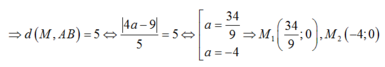

Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến

Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)

Khoảng cách AM là nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của A lên \(\Delta\)
Gọi d là đường thẳng qua A và vuông góc \(\Delta\Rightarrow\) d nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
M là giao điểm của d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+y-2=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)

Đáp án D
Đường thẳng đi qua 2 điểm A và B có vectơ chỉ phương là ![]() suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
Suy ra phương trình AB: 4( x-3) + 3( y+ 1) = 0 hay 4x+ 3y -9=0
Do M nằm trên Ox nên M( x; 0)
Do d(M; AB)=1 nên
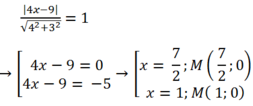

Gọi M(x,y)
Theo bài ra ta có:
d(M,AB)=\(\frac{x-3y+5}{\sqrt{10}}\) =\(\frac{\sqrt{10}}{2}\)
=>x=3y (1)
CosAMB=\(\frac{y^2-5y+6+x^2-5x+4}{\sqrt{\left(y-2\right)^2+\left(1-x\right)^2}\cdot\sqrt{\left(y-3\right)^2+\left(4-x\right)^2}}\) =\(-\frac{\sqrt{2}}{2}\) (2)
thay (1) vào (2) có lẽ ra pt bậc 4 đó giải tiếp nhé
thank nha