Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Hai điểm A(1;2) và B(4;6) ⇒ AB = 5
Gọi M(0;m).
Vì diện tích tam giác MAB bằng 1
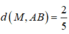
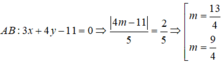

ĐÁP ÁN B.
Do C nằm trên đường thẳng ∆: x – 2y + 3 = 0 nên ta gọi tọa độ C là C(2y – 3; y).
Mà A B = ( − 2 + 4 ) 2 + ( 1 + 1 ) 2 = 2 2
Phương trình AB: qua A( - 4; -1) và nhận VTCP A B → ( 2 ; 2 ) nên có VTPT là: n → ( 1 ; − 1 ) :
1( x+ 4) – 1 ( y + 1) = 0 hay x – y + 3 = 0
d ( C ; A B ) = 2 y − 3 − y + 3 2 = y 2
Theo đầu bài ta có:
40 = S = 1 2 . A B . d ( C ; A B ) = 1 2 . 2 2 . y 2 ⇔ y = 40 ⇔ y = ± 40

\(\overrightarrow{AB}=\left(3;-3\right)\Rightarrow AB=3\sqrt{2}\)
\(S_{MAB}=\dfrac{1}{2}d\left(M;AB\right).AB=3\Rightarrow D\left(M;AB\right)=\dfrac{6}{AB}=\sqrt{2}\)
Phương trình AB:
\(1\left(x-0\right)+1\left(y-1\right)=0\Leftrightarrow x+y-1=0\)
\(M\in Oy\Rightarrow M\left(0;y\right)\Rightarrow d\left(M;AB\right)=\dfrac{\left|y-1\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
\(\Rightarrow\left|y-1\right|=2\Rightarrow\left[{}\begin{matrix}m=-1\\n=3\end{matrix}\right.\)

\(\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)\Rightarrow AB=2\sqrt{5}\)
Đường thẳng AB nhận (1;-2) là 1 vtpt nên pt có dạng:
\(1\left(x+1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+5=0\)
\(\overrightarrow{AC}=\left(2;-8\right)=2\left(1;-4\right)\Rightarrow AC=2\sqrt{17}\)
Đường thẳng AC nhận (4;1) là 1 vtpt nên pt có dạng:
\(4\left(x+1\right)+1\left(y-2\right)=0\Leftrightarrow4x+y+2=0\)
Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}S_{MAB}=\dfrac{1}{2}d\left(M;AB\right).AB\\S_{MAC}=\dfrac{1}{2}d\left(M;AC\right).AC\end{matrix}\right.\)
\(S_{MAB}=S_{MAC}=d\left(M;AB\right).AB=d\left(M;AC\right).AC\)
\(\Leftrightarrow\dfrac{\left|x-2y+5\right|}{\sqrt{1+\left(-2\right)^2}}.2\sqrt{5}=\dfrac{\left|4x+y+2\right|}{\sqrt{4^2+1^2}}.2\sqrt{17}\)
\(\Leftrightarrow\left|x-2y+5\right|=\left|4x+y+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+y+2=x-2y+5\\4x+y+2=-x+2y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y-1=0\\5x-y+7=0\end{matrix}\right.\)
Vậy quỹ tích M là 2 đường thẳng có pt: \(\left[{}\begin{matrix}x+y-1=0\\5x-y+7=0\end{matrix}\right.\)

a: Vì (d) đi qua A(3;-4) và (0;2) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-4\\b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
b: vì (d)//y=-4x+4 nên a=-4
Vậy:(d): y=-4x+b
Thay x=-2 và y=0 vào (d), ta được:
b+8=0
hay b=-8

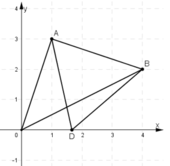
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
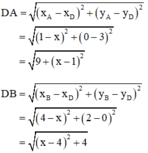
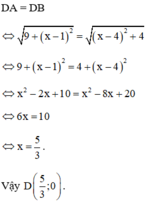
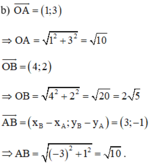
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
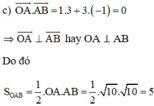

Chọn C.
Điểm M ∈ Ox ⇒ M(x; 0).
Khi đó ![]()
ΔMAB vuông tại M nên ![]()
Hay (–3 – x)(4 – x) + 2.3 = 0
⇔ –12 + 3x – 4x + x2 + 6 = 0
⇔ x2 – x – 6 = 0 ⇔ 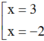 .
.
Vậy: M1(3; 0), M2(-2; 0) và tổng hoành độ của chúng là : 3 + (-2) = 1.

Đường tròn \((C)\) tâm \(I(a;b)\) bán kính \(R\)có phương trình
\((x-a)^2+(y-b)^2=R^2.\)
\(∆MAB ⊥ M\) \(\rightarrow \) \(AB\) là đường kính suy ra \(∆\) qua \(I\) do đó:
\(a-b+1=0 (1)\)
Hạ \(MH⊥AB\) có \(MH=d(M, ∆)= \dfrac{|2-1+1|}{\sqrt{2}}={\sqrt{2}} \)
\(S_{ΔMAB}=\dfrac{1}{2}MH×AB \Leftrightarrow 2=\dfrac{1}{2}2R\sqrt{2} \)
\(\Rightarrow R = \sqrt{2} \)
Vì đường tròn qua\(M\) nên (\(2-a)^2+(1-b)^2=2 (2)\)
Ta có hệ :
\(\begin{cases} a-b+1=0\\ (2-a)^2+(1-b)^2=0 \end{cases} \)
Giải hệ \(PT\) ta được: \(a=1;b=2\).
\(\rightarrow \)Vậy \((C) \)có phương trình:\((x-1)^2+(y-2)^2=2\)
Đáp án C
+ Ta có: A B → = ( 3 ; 4 ) và AB= 5.
Do điểm M nằm trên trục tung nên tọa độ điểm M có dạng M(0; y)
+Khi đó diện tích tam giác MAB là S = 1 2 . A B . d ( M ; A B )
Thay số 1= 1/2.5.d( M; AB) nên d ( M ; A B ) = 2 5
+ Viết phương trình đường thẳng AB: đi qua A( 1; 2) và nhận A B → = ( 3 ; 4 ) làm VTCP nên nhận n → ( 4 ; - 3 ) làm VTPT.
Suy ra phương trình tổng quát: 4( x-1)- 3( y-2) =0
Hay 4x- 3y+ 2= 0
+ ta có:
+ TH1: nếu -3y+ 2= 2 thì y= 0 và M( 0;0)
+ TH2: Nếu -3y+ 2= -2 thì y=4/3 và M( 0; 4/3).