Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xet ΔAEH và ΔACE có
góc AEH=góc ACE
góc EAH chung
=>ΔAEH đòng dạng vói ΔACE
=>AE^2=AH*AC
Xét ΔAEB và ΔACE có
góc AEB=góc ACE
góc EAB chung
=>ΔAEB đồng dạng với ΔACE
=>AE^2=AB*AC

a, b, c HS tự làm
d, Gợi ý: G' ÎOI mà I G ' I O = 1 3 => G' thuộc (G'; 1 3 R)

Gọi A' là giao điểm của đường tròn ngoại tiếp tam giác AEF và tia AB
Ta chứng minh được E,A,N và M, A, F thẳng hàng
=> A đối xứng với A' qua C => B đối xứng với A' qua điểm A mà A' cố định
=> Tâm I của đường tròn ngoại tiếp tam giác BMN nằm trên đường trung trực của đoạn thẳng BA'.

b) Trong (O) có EF là dây cung không đi qua O và K là trung điểm EF
\(\Rightarrow OK\bot EF\Rightarrow\angle OKM=90=\angle ODM\Rightarrow OKDM\) nội tiếp
mà theo câu a) MCOD nội tiếp nên M,D,K,O,C cùng thuộc 1 đường tròn
\(\Rightarrow MDKC\) nội tiếp
\(\Rightarrow\angle MKD=\angle MCD=\angle MDC\) (\(\Delta MCD\) cân tại M) \(=\angle MKC\)
\(\Rightarrow KM\) là phân giác \(\angle DKC\)
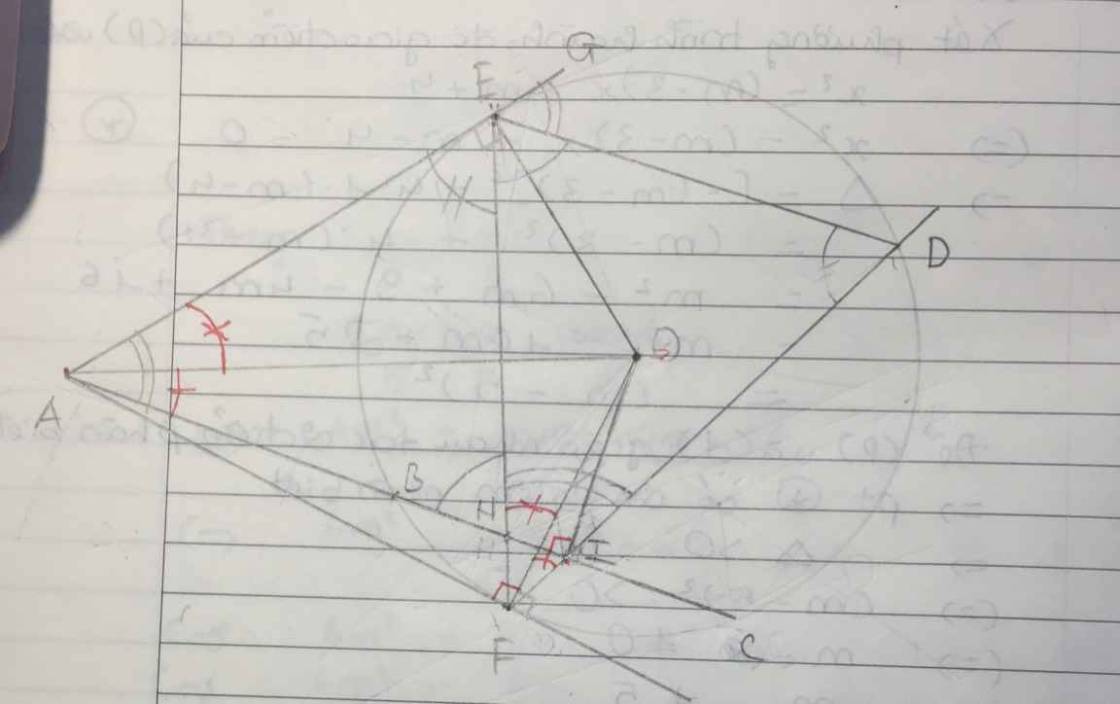
Cho mk xin cái hình mk giải cho