Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


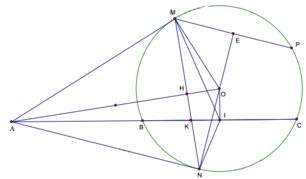
gọi Ex là tia đối của tiếp tuyến EA
Ta có : \(\widehat{xED}=\frac{1}{2}sđ\widebat{ED}\); \(\widehat{EFD}=\frac{1}{2}sđ\widebat{ED}\)\(\Rightarrow\widehat{xED}=\widehat{EFD}\)( 1 )
Dễ thấy tứ giác AFOE nội tiếp
I là trung điểm của BC nên OI \(\perp\)BC \(\Rightarrow\)tứ giác AIOE nội tiếp
\(\Rightarrow\)5 điểm A,F,I,O,E cùng thuộc 1 đường tròn
\(\Rightarrow\)tứ giác AFIE nội tiếp \(\Rightarrow\)\(\widehat{EAI}=\widehat{EFI}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\widehat{xED}=\widehat{EAI}\Rightarrow ED//AC\)
Gọi N là giao điểm của AO và EF
Dễ chứng minh AN \(\perp\)EF
\(\DeltaẠNH~\Delta AIO\left(g.g\right)\Rightarrow\frac{AN}{AH}=\frac{AI}{AO}\Rightarrow AI.AH=AN.AO\)( 3 )
Ta có : \(AE^2=AN.AO\)( 4 )
Xét \(\Delta AEB\)và \(\Delta ACE\)có :
\(\widehat{EAC}\)( chung ) ; \(\widehat{AEB}=\widehat{ACE}=\frac{1}{2}sđ\widebat{EB}\)
\(\Rightarrow\Delta AEB~\Delta ACE\left(g.g\right)\)
\(\Rightarrow\frac{AE}{AB}=\frac{AC}{AE}\Rightarrow AE^2=AB.AC\)( 5 )
Từ ( 3 ) , ( 4 ) và ( 5 ) suy ra : AH.AI = AB.AC
đề bạn cho thiếu nhé. đoạn cuối AH. AI = AB . AC với H là giao điểm của AC và EF

2 tam giác HIE và HFA đồng dạng do có góc tại đỉnh H bằng nhau và góc HIE = góc FA (cùng chắn cung A của Q) => HI / HF = HE / HA => HI*HA = HE*HF ♦
2 ∆ HEB và HCF đồng dạng do có góc tại đỉnh H bằng nhau và góc HEB = góc HCF (cùng chắn cung BF của O) => HE / HC = HB / HF => HB*HC = HE*HF ♥
(Nếu bạn đã học phương tích của điểm đối với đường tròn thì có ngay ♦ và ♥ không cần cm vì ♦ chính là pt của H đối với Q còn ♥ là pt của H đối với O)
♦, ♥ => HI*HA = HB*HC => HI*(AI - HI) = (x - HI)(x + HI) => HI*AI = x²
=> HI = x² / AI = hằng số (A, I cố định nên AI không đổi)
=> H cố định.
Dễ thấy OIHK nội tiếp đường tròn (P) => đường tròn ngoại tiếp ∆ IOK chính là (P). Tâm đường tròn (P) dĩ nhiên nằm trên trung trực k của HI mà trung trực này cố định do H, I cố định. Vậy tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc k cố định

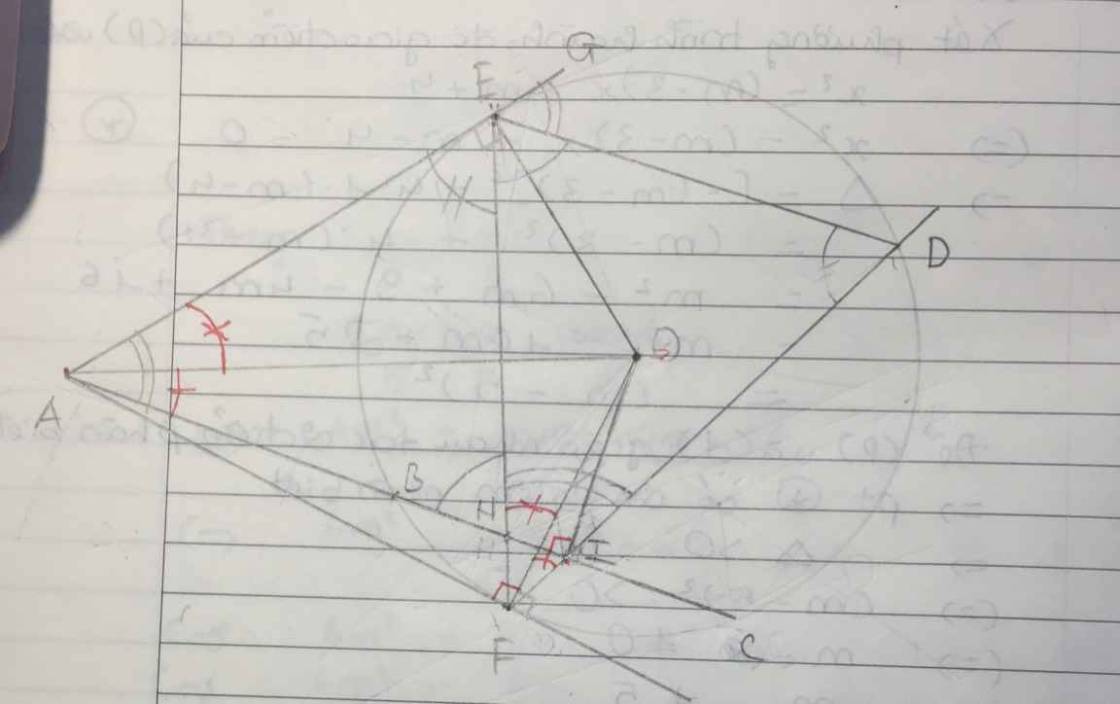
2 A K = 1 A B + 1 A C ⇔ 2 A B . A C = A K ( A B + A C ) ⇔ A B . A C = A K . A I
(Do AB+ AC = 2AI)
∆ABN đồng dạng với ∆ANC => AB.AC = AN2
∆AHK đồng dạng với ∆AIO => AK.AI = AH.AO
Tam giác ∆AMO vuông tại M có đường cao MH => AH.AO = AM2
=> AK.AI = AM2 . Do AN = AM => AB.AC = AK.AI

a:Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
b: Xét ΔOBA vuông tại B có BH là đường cao
nên \(BH^2=OH\cdot HA=\left(\dfrac{BC}{2}\right)^2=\dfrac{BC^2}{4}\)
b: Xet ΔAEH và ΔACE có
góc AEH=góc ACE
góc EAH chung
=>ΔAEH đòng dạng vói ΔACE
=>AE^2=AH*AC
Xét ΔAEB và ΔACE có
góc AEB=góc ACE
góc EAB chung
=>ΔAEB đồng dạng với ΔACE
=>AE^2=AB*AC