K
Khách

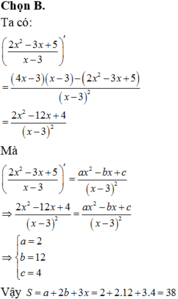
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
TQ
Trần Quang Hiếu
20 tháng 3 2016
bài 3: tính nhanh:a) -5 phần 9 + 3 phần 5 - 3 phần 9 + -2 phần 5b) 5 phần 17 - 9 phần 15 - 2 phần 17 + -2 phần 5c) ( 1 phần 9 - 9 phần 17 ) + 3 phần 6 - ( 12 phần 17 - 1 phần 2 ) + 5 phần 9bài 4: tìm xa) 3 phần 4 - x = 1b) x + 4 = 1 phần 5c) x phần 4 - 3 phần 7 + 2 phần 5 = 31 phần 140Toán 6 ! giúp mình đi mình tick cho các bạn! d) 5 phần 12 + 5 phần x - 1 phần 8 = 1 phần...
Đọc tiếp

bài 3: tính nhanh:

a) -5 phần 9 + 3 phần 5 - 3 phần 9 + -2 phần 5

b) 5 phần 17 - 9 phần 15 - 2 phần 17 + -2 phần 5

c) ( 1 phần 9 - 9 phần 17 ) + 3 phần 6 - ( 12 phần 17 - 1 phần 2 ) + 5 phần 9

bài 4: tìm x

a) 3 phần 4 - x = 1

b) x + 4 = 1 phần 5

c) x phần 4 - 3 phần 7 + 2 phần 5 = 31 phần 140

Toán 6 ! giúp mình đi mình tick cho các bạn!

 

d) 5 phần 12 + 5 phần x - 1 phần 8 = 1 phần 2
#Mẫu giáo
11
KN
Kiên NT
20 tháng 3 2016

dễ khủng khíp , động não chút đi

Đúng(1)
TQ
Trần Quang Hiếu
20 tháng 3 2016

THÌ HÃY LÀ HỘ ĐI

 

Đúng(0)
TH
Thanh Huyền
16 tháng 2 2016
Cho đa thức:          \(A\left(x\right)=2x^5-4x^3+x^2-2x+2\)          \(B\left(x\right)=x^5-2x^4+x^2-5x+3\)          \(C\left(x\right)=x^4+4x3+3x^2-8x+4\frac{3}{16}\)a. Tính \(M\left(x\right)=A\left(x\right)-2B\left(x\right)+C\left(x\right)\)b. Tính giá trị của M(x) khi \(x=-\sqrt{0,25}\)c. Có giá trị nào của x để M(x) = 0 không...
Đọc tiếp

Cho đa thức:

          \(A\left(x\right)=2x^5-4x^3+x^2-2x+2\)

          \(B\left(x\right)=x^5-2x^4+x^2-5x+3\)

          \(C\left(x\right)=x^4+4x3+3x^2-8x+4\frac{3}{16}\)

a. Tính \(M\left(x\right)=A\left(x\right)-2B\left(x\right)+C\left(x\right)\)

b. Tính giá trị của M(x) khi \(x=-\sqrt{0,25}\)

c. Có giá trị nào của x để M(x) = 0 không ? 
#Mẫu giáo
1
L
Lovers
16 tháng 2 2016

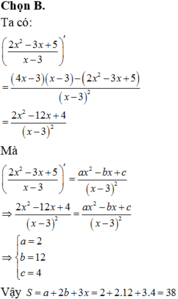
a) Ta có:

\(M\left(x\right)=A\left(x\right)-2.B\left(x\right)+C\left(x\right)\)

\(=\left(2x^5-4x^3+x^2-2x+2\right)-2.\left(x^5-2x^4+x^2-5x+3\right)+\left(x^4+3x^3+3x^2-8x+4\frac{3}{16}\right)\)

\(=2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-6+x^4+4x^3+3x^2-8x+\frac{67}{16}\)

\(=\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-6+\frac{67}{16}\right)\)

\(=0+5x^4+0+2x^2+0+\frac{3}{16}\)

\(=5x^4+2x^2+\frac{3}{16}\)

b) Thay  \(x=-\sqrt{0,25}=-0,5\); ta có:

\(M\left(-0,5\right)=5.\left(-0,5\right)^4+2.\left(-0,5\right)^2+\frac{3}{16}\)

\(=5.0,0625+2.0,25+\frac{3}{16}\)

\(=\frac{5}{16}+\frac{8}{16}+\frac{3}{16}=\frac{16}{16}=1\)

c) Ta có:

\(x^4\ge0\) với mọi x

\(x^2\ge0\) với mọi x

\(\Rightarrow5x^4+2x^2+\frac{3}{16}>0\) với mọi x

Do đó không có x để M(x)=0

Đúng(0)
DH
Đỗ Hoàng Ngọc
24 tháng 4 2016

Cho 2 đa thức

A(x)= -x^2-3+5x^4-1/3x^3+1

B(x)= -3/4x^3+2-x^2+4x

a) Sắp xếp theo lũy thừa giảm dần của biến

b) Tính A(x)+B(x)

c) x=1 là nghiệm của đa thức A(x)+B(x)? Vì sao?
#Mẫu giáo
1
NL
Nguyễn Lâm Ngọc
24 tháng 4 2016

a) A(x)= 5x^4-1/3x^3-x^2-2

B(x)= -3/4x^3-x^2+4x+2

b) A(x)+B(x)=17/4x^3-1/3x^3-2x^2+4x

                    =47/12x^3-2x^2+4x

c) thay x= 1 vao đt A(x)+B(x) ta có:

A(x)+B(x)=47/12*1^3-2*1^2+4*1

                =71/12

Vậy x = 1 ko phai là nghiệm của đt A(x)+B(x)

nếu tính toán ko sai thì chắc như thếucche

Đúng(0)
PT
Pham Trong Bach
3 tháng 3 2017
Trong không gian với hệ tọa độ Oxyz, cho điểm A(3;1;3), mặt phẳng (P):x+y+z-7=0 và đường thẳng (d): x - 1 2 = y 1 = z 3 . Mặt cầu (S) có tâm I(a;b;c) thuộc (P), bán kính R= 6 và tiếp xúc với (d) tại A với a,b,c là các số thực dương. Giá trị của biểu thức a+2b+3c bằng A. 11. B. 17. C. 16....
Đọc tiếp

Trong không gian với hệ tọa độ Oxyz, cho điểm A(3;1;3), mặt phẳng (P):x+y+z-7=0 và đường thẳng (d): x - 1 2 = y 1 = z 3 . Mặt cầu (S) có tâm I(a;b;c) thuộc (P), bán kính R= 6 và tiếp xúc với (d) tại A với a,b,c là các số thực dương. Giá trị của biểu thức a+2b+3c bằng

A. 11.

B. 17.

C. 16.

D. 12.
#Mẫu giáo
1
CM
Cao Minh Tâm
3 tháng 3 2017

Đúng(0)
PT
Pham Trong Bach
6 tháng 9 2019
Cho log 7 12 = x ;    log 12 24 = y và log 54 168 = a   x y + 1 b x y + c x trong đó a, b, c là các số  nguyên. Tính giá trị của biểu thức S = a + 2 b + 3 c   A. S = 4 B. S = 19 C. S = 10 D. S =...
Đọc tiếp

Cho log 7 12 = x ;    log 12 24 = y và log 54 168 = a   x y + 1 b x y + c x trong đó a, b, c là các số  nguyên. Tính giá trị của biểu thức S = a + 2 b + 3 c  

A. S = 4

B. S = 19

C. S = 10

D. S = 15
#Mẫu giáo
1
CM
Cao Minh Tâm
6 tháng 9 2019

Đáp án D

Đúng(0)
PT
Pham Trong Bach
1 tháng 11 2019
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) ,  trong đó a > 0 , b > 0 , c > 0  và 3 a + 1 b + 3 c = 5 .  Biết mặt phẳng...
Đọc tiếp

Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) ,  trong đó a > 0 , b > 0 , c > 0  và 3 a + 1 b + 3 c = 5 .  Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 ,  khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?

A .   ( 0 ; 1 2 ) .

B. (0;1).

C. (1;3).

D. (4;5).
#Mẫu giáo
1
CM
Cao Minh Tâm
1 tháng 11 2019

Chọn C.

Đúng(0)
PT
Pham Trong Bach
2 tháng 6 2018
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng  ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng  α tiếp xúc với mặt cầu (S): ( x ...
Đọc tiếp

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng  ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng  α tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 72 7 . Thể tích khối OABC với O là gốc tọa độ bằng

A.  2 9

B.  3 4

C.  1 8

D.  4 3

#Mẫu giáo
1
CM
Cao Minh Tâm
2 tháng 6 2018

Đúng(0)
NT
Nguyễn Thị Hoài An
9 tháng 3 2016
bài 1: Tìm x biết | x - 3 | = 2x+1bài 2: Tìm tập nghiệm biểu diễn trên trục số | x+ 3 | > 3bài 3: Tìm giá trị nhỏ nhất của a) | 2x - 1 | - 10b) | x+ 2015 | + | x+ 2016 |bài 4: Tìm n nguyên để P = \(\frac{2n+1}{n-2}\)nguyênbài 5: Cho \(\frac{a}{2}\) = \(\frac{b}{3}\) ; \(\frac{b}{2}\) = \(\frac{c}{5}\) và 2a-2b+ c= 121Tính a, b, cb) Cho b2 = ac. CMR: \(\frac{a^2+b^2}{b^2+c^2}\) = \(\frac{a}{c}\)Giúp mình đi mình đang cần...
Đọc tiếp

bài 1: Tìm x biết | x - 3 | = 2x+1

bài 2: Tìm tập nghiệm biểu diễn trên trục số | x+ 3 | > 3

bài 3: Tìm giá trị nhỏ nhất của 

a) | 2x - 1 | - 10

b) | x+ 2015 | + | x+ 2016 |

bài 4: Tìm n nguyên để P = \(\frac{2n+1}{n-2}\)nguyên

bài 5: Cho \(\frac{a}{2}\) = \(\frac{b}{3}\) ; \(\frac{b}{2}\) = \(\frac{c}{5}\) và 2a-2b+ c= 121

Tính a, b, c

b) Cho b2 = ac. CMR: \(\frac{a^2+b^2}{b^2+c^2}\) = \(\frac{a}{c}\)

Giúp mình đi mình đang cần gấp

Ai làm nhanh và đúng mình sẽ tick cho 
#Mẫu giáo
5
NT
Nguyễn Thị Hoài An
9 tháng 3 2016

lam nhanh giup minh nha minh se tick cho

Đúng(0)
NT
Nguyễn Thắng Tùng
9 tháng 3 2016

nhiều bài quá mình chỉ làm được bài 1,3,4,5

bài 2 mình đang suy nghĩ

bạn có thể vào Hỏi đáp Toánđể hỏi bài !

Đúng(0)
I
IzanamiAiko123
11 tháng 9 2019 - olm

Rút gọn biểu thức

a) A= (2x-5)2-4x(x-6)

b) B= (7x-3y)2-(7x-3y)(7x+3y)

c) C= (3-2x)2+(3+2x)2

d) D= (x-y+z)2+(z-y)2+2(x-y+z)(y-z)

MÌNH CẦN GẤP LẮM, MẤY BẠN GIÚP MÌNH NHA. HỨA SẼ TICK CHO BẠN NÀO LÀM NHANH NHẤT Ạ!!
#Mẫu giáo
1
NL
Nguyễn Linh Chi
11 tháng 9 2019

\(A=\left(2x\right)^2-2.2x.5+5^2-4x.x+4x.6\)

\(=4x^2-20x+25-4x^2+24x=4x+25\)

\(B=\left(7x-3y\right)^2-\left(7x-3y\right)\left(7x+3y\right)\)

\(=\left(7x-3y\right)\left(7x-3y-7x-3y\right)\)

\(=\left(7x-3y\right)\left(-6y\right)=18y^2-42xy\)

\(C=\left(3-2x\right)^2+\left(3+2x\right)^2\)

\(=9-2.3.2x+4x^2+9+2.3.2x+4x^2\)

\(=18+8x^2\)

\(D=\left(x-y+z\right)^2+\left(z-y\right)^2+2\left(x-y+x\right)\left(y-z\right)\)

\(=\left(x-y+z+z-y\right)^2=x^2\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP