Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
+ Lần 2: vật đi từ biên về VTCB (lực phục hồi đổi chiều) y = T/4. Do
![]()
+ Lần 1: vật đi từ biên về Δlo (lực đàn hồi = 0) là T/6 => A = 2Δlo =>
![]()

Đáp án D.
Lực phục hồi đổi chiều tại VTCB. Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
Lần thứ hai: khi đưa vật về vị trí lò xo không biến dạng rồi thả nhẹ thì quãng đường vật chuyển động đến lúc lực phục hồi đổi chiều (VTCB) bằng A, tương ứng với thời gian vật chuyển động bằng T/4

Lần thứ nhất: khi nâng vật lên rồi thả nhẹ vật chuyển động trên vị trí lực đàn hồi triệt tiêu tức là vật đã chuyển động từ vị trí biên (có ly độ x = -A) đến vị trí có ly độ x = - ∆ l 0 (chọn chiều dương Ox hướng xuống)
Do thời gian
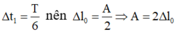
Vậy tỉ số gia tốc vật và gia tốc trọng trường ngay khi thả lần thứ nhất là
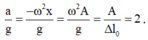 .
.

Đáp án B
+ Độ biến dạng của lò xo tại vị trí cân bằng
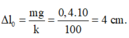
+ Đưa vật đến vị trí lò xo không biến dạng rồi thả nhẹ
![]()
+ Động năng của vật bằng thế năng lần đầu tiên tại vị trí
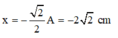
(trục Ox thẳng đứng, hướng xuống).
Lực đàn hồi có độ lớn
![]()

Chọn A
Chọn trục tọa độ có phương thẳng đứng, chiều dương từ trên xuống dưới.
+ A = 2Dl
+ Vị trí thả vật là x1 = +A và vị trí lò xo không biến dạng là x2 = - Dl = -A/2.
+ Sử dụng thang thời gian:
t = tA→O + tO→- A/2
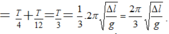

Phương pháp: Sử dụng công thức tính độ dãn của lò xo treo thẳng đứng
Cách giải:
Biên độ ban đầu :

Đáp án C
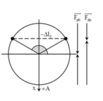


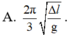
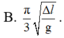
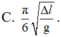
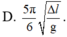

Cả hai lần thả, hệ lò xo đều dao động điều hòa với chu kỳ T (s)
+) Xét lần thả thứ 2, ta thấy khoảng thời gian y là khoảng mà vật chuyển động từ biên -A đền vị trí có ly độ 0, suy ra \(y=\frac{T}{4}\)
+) Xét lần thả thứ nhất,
\(\frac{x}{y}=\frac{2}{3}\Rightarrow x=\frac{T}{6}\)
\(\Rightarrow\) x là khoảng thời gian vật di chuyển từ ly độ -A đền ly độ -A/2
Theo đề bài \(\Rightarrow\) vị trí -A/2 là vị trí lực đàn hồi triệt tiêu
\(\Rightarrow\frac{A}{2}=\Delta l_0=\frac{mg}{k}\Rightarrow A=\frac{2mg}{k}\)
Vậy tỷ số cần tìm là \(\frac{a_{max}}{g}=\frac{A\omega^2}{g}=\frac{\frac{2mg}{k}.\frac{k}{m}}{g}=2\)