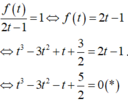Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do \(\lim\limits_{x\rightarrow-1}\dfrac{2f\left(x\right)+1}{x+1}=5\) hữu hạn nên \(2f\left(x\right)+1=0\) phải có nghiệm \(x=-1\)
\(\Leftrightarrow2f\left(-1\right)=-1\Leftrightarrow f\left(-1\right)=-\dfrac{1}{2}\)
Đoạn dưới tự hiểu là \(\lim\limits_{x\rightarrow-1}\) (vì kí tự lim rất rắc rối)
\(I=\dfrac{\left[4f\left(x\right)+3\right]\left[\sqrt{4f^2\left(x\right)+2f\left(x\right)+4}-2\right]+2\left[4f\left(x\right)+3\right]-2}{x^2-1}\)
\(=\dfrac{\left[4f\left(x\right)+3\right]\left[4f^2\left(x\right)+2f\left(x\right)\right]}{\left(x+1\right)\left(x-1\right)\left[\sqrt{4f^2\left(x\right)+2f\left(x\right)+4}+2\right]}+\dfrac{4\left[2f\left(x\right)+1\right]}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{2f\left(x\right)+1}{x+1}.\dfrac{f\left(x\right).\left[4f\left(x\right)+3\right]}{x-1}+\dfrac{2f\left(x\right)+1}{x+1}.\dfrac{4}{x-1}\)
\(=5.\dfrac{f\left(-1\right).\left[4f\left(-1\right)+3\right]}{-2}+5.\dfrac{4}{-2}=\dfrac{5.\left(-\dfrac{1}{2}\right)\left(-2+3\right)}{-2}+5.\dfrac{4}{-2}=...\)
Không phải dạng, nó chỉ là ứng dụng kiến thức cơ bản về giới hạn của hàm thôi

\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-16}{x-1}\) hữu hạn nên \(f\left(x\right)-16=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)=16\)
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-16}{x-1}.\dfrac{1}{\sqrt{2f\left(x\right)+4}+6}=24.\dfrac{1}{\sqrt{2.16+4}+6}=2\)

Chọn B.
D = [-2; 2]
F(x) không xác định tại x = 3
![]() ; f(-2) = 0. Vậy hàm số liên tục tại x = -2
; f(-2) = 0. Vậy hàm số liên tục tại x = -2
![]()
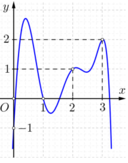
Vậy không tồn tại giới hạn của hàm số khi x → 2.